决策树

发表于 | 分类于

决策树是一种非常常用的数据挖掘算法。以分类问题为例，它根据一系列子问题形成树结构进行决策，这也是人类在面临决策问题时一种很自然的处理机制，因此是也是知识图谱的重要算法之一。该算法采用的是分而治之（divide-and-conquer）的思想。本文主要介绍决策树中的ID3算法。

基本原理及算法

香农熵/信息熵

信息熵（information entropy）是度量样本集合纯度最常用的一个指标，假定当前样本集合\(D\)中第\(k\)类样本所占的比例为\(p_k\)（k=1,2,...,K），则\(D\)的信息熵定义为： \[Ent(D) = - \sum_{k=1}^{K} p_k log_2{p_k}\] Ent(D)的值越小，样本集合\(D\)的纯度越高。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from math import log

def calcShannonEnt(dataSet):
    """
    计算根节点的熵
    """
    numEntries = len(dataSet) # 训练数据的样本个数
    labelCounts = {}
    
    for featVec in dataSet:
        currentLabel = featVec[-1] # 最后一列表示当前样本的标签，可以是数字或字符串
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob*log(prob, 2)
    return shannonEnt
1
2
3
4
5
6
7
8
def createDataSet():
    dataSet = [[1, 1, 'yes'],
              [1, 1, 'yes'],
              [1, 0, 'no'],
              [0, 1, 'no'],
              [0, 1, 'no']]
    labels = ['no surfacing', 'flippers'] # 只是表示数据集中前两列表示的特征含义，而不是标签（标签在dataSet最后一列中）
    return dataSet, labels
1
myData, labels = createDataSet()
1
myData
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
1
calcShannonEnt(myData)
0.9709505944546686
1
2
# 正概率和负概率组合
-(2/5*log(2/5,2)+3/5*log(3/5,2))
0.9709505944546686
1
2
3
# 增加一种类别
myData[0][-1] = 'maybe'
myData
[[1, 1, 'maybe'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]

熵越高，数据的纯度越低

1
calcShannonEnt(myData) # 熵越高，数据的纯度越低
1.3709505944546687

划分数据集

信息增益用来衡量用属性\(a\)划分数据集所获得的“纯度提升”。信息增益越大，“纯度提升”越大。

假定离散属性\(a\)有\(V\)个可能的取值\({a^1, a^2, ..., a^V}\)，若使用属性\(a\)来对样本集\(D\)进行划分，则会产生\(V\)个分支节点，其中第\(v\)个分支包含了属性\(a\)取值为\(a^v\)的样本集合\(D^v\)。根据信息熵的定义，可以计算样本集合\(D^v\)的信息熵。再考虑到不同的分支节点所包含的样本数不同，给各个分支节点取权重\(|D|^v/|D|\)，即样本数越多的分支节点的影响越大，因此可以计算出用属性\(a\)对样本进行划分所获得的“信息增益”: \[Gain(D, a) = Ent(D) - \sum_{v=1}^{V} \frac{|D^v|}{|D|}Ent(D^v)\] 划分数据集所选择的属性应当满足： \[a_* = arg max_{a \in A} Gain(D, a)\] 使得每个分支节点的数据集熵\(Ent(D^v)\)最小化（纯度最大化）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def splitDataSet(dataSet, axis, value):
    """
    划分数据
    dataSet: 待划分的数据集
    axis: 划分数据集的特征
    value: 需要返回特征的值
    """
    retDataSet = []
    for featVec in dataSet:
        ### 提取数据
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis] # axis前的所有特征
            reducedFeatVec.extend(featVec[axis+1:]) # axis后的所有特征，扩展后，去除了特征axis的信息
            retDataSet.append(reducedFeatVec) # 将所有特征axis值为value的样本合并，最后输出
    return retDataSet
1
2
myDat, labels = createDataSet()
myDat
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
1
splitDataSet(myDat, 0, 1)
[[1, 'yes'], [1, 'yes'], [0, 'no']]
1
splitDataSet(myDat, 0, 0)
[[1, 'no'], [1, 'no']]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def choosBestFeatureTopSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1 # 除最后一列是label外，其余列都是属性
    baseEntropy = calcShannonEnt(dataSet) # 根节点的熵
    bestInfoGain = 0.0; bestFeature = -1
    
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet] # 所有样本的第i个属性
        uniqueVals = set(featList) # 转化为集合类型，输出列表featList中唯一元素组成的列表
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature
1
choosBestFeatureTopSplit(myDat)
0

递归构建决策树

工作原理： 1. 输入原始数据集 2. 根据信息增益最大化准则选择最优属性 3. 根据最优属性划分数据集 4. 第一次划分之后再次划分

递归终止条件： 1. 遍历所有属性 2. 每个分支下的所有样本属于同一类

1
2
3
4
5
6
7
8
9
10
11
12
13
import operator
def majorityCnt(classList):
    """
    投票表决，与kNN代码中的classify0类似，返回出现频次最多的标签
    """
    classCount = {}
    
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.item(), \
                             key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def createTree(dataSet, labels):
    """
    dataSet: 输入数据集，大小m*nc，其中第nc-1列为label
    labels: 属性名称，大小1*(nc-1)
    """
    classList = [example[-1] for example in dataSet] # 数据集最后一列是标签，提取标签，组成list
    if classList.count(classList[0]) == len(classList): # 当标签list的第一个标签的样本数和所有的样本数相等时，表示所有样本都是属于同一类
        return classList[0] # 满足第二个终止条件，返回类名
    if len(dataSet[0]) == 1: # 当最后只剩下一种属性时
        return majorityCnt(classList) # 投票选择数量最多的类作为输出
    bestFeat = choosBestFeatureTopSplit(dataSet) # 选择最优属性划分数据，返回属性所在的位置
    bestFeatLabel = labels[bestFeat] # 提取最优属性的名称
    myTree = {bestFeatLabel:{}} # 生成一级节点
    del(labels[bestFeat]) # 删除最优属性对应的名称
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues) # 提取最优属性的唯一取值序列
    
    for value in uniqueVals:
        subLabels = labels[:] # 引用删除最优属性后的属性名称列表
        # 利用最优属性对数据进行分割，属性名为key，对应的值作为value，接着对分割后的数据集进行数据划分，递归调用。
        myTree[bestFeatLabel][value] = createTree(splitDataSet \
                                                 (dataSet, bestFeat, value), subLabels)
        
    return myTree
1
2
3
myDat, labels = createDataSet()
myTree = createTree(myDat, labels)
myTree
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

绘制树形图

和kNN不同，决策树算法的数据形式含义十分清晰，可以借助画图工具将其绘制出来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        else: numLeafs += 1
    return numLeafs

def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else: thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth
1
2
print(getNumLeafs(myTree))
print(getTreeDepth(myTree))
3
2
1
2
a = list(myTree.keys())[0]
myTree[a]
{0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
import matplotlib.pyplot as plt

# 定义文本框和箭头格式
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")

# 绘制带箭头的注解
def plotNode(nodeText, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeText, xy=parentPt, \
                            xycoords='axes fraction', \
                            xytext=centerPt, textcoords='axes fraction', \
                           va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)

def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0] - cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString)
    
def plotTree(myTree, parentPt, nodeTxt):
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, \
             plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            plotTree(secondDict[key],cntrPt,str(key))
        else:
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), \
                    cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
    
    
def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
    plotTree(inTree, (0.5, 1.0), '')
    plt.show()
1
createPlot(myTree)
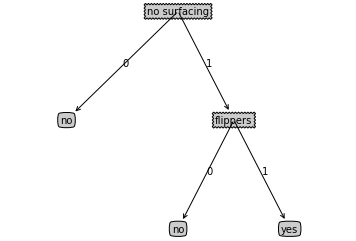
简单的树形图

简单的树形图

使用决策树进行分类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def classify(inputTree, featLabels, testVec):
    """
    使用决策树进行分类
    inputTree: 利用训练数据构建好的决策树
    featLabels: 特征的含义
    testVec: 输入的测试数据
    """
    firstStr = list(inputTree.keys())[0] # 提取第一个属性
    secondDict = inputTree[firstStr] # 提取第一个属性对应的值
    featIndex = featLabels.index(firstStr) # 提取第一个属性对应的索引
    for key in secondDict.keys(): 
        if testVec[featIndex] == key:
            if type(secondDict[key]).__name__ == 'dict':
                classLabel = classify(secondDict[key], featLabels, testVec)
            else: classLabel = secondDict[key]
    return classLabel
1
2
3
4
5
6
7
def retrieveTree(i):
    listOfTrees = [{'no surfacing': {0: 'no', 1: {'flippers': \
                                                {0: 'no', 1: 'yes'}}}},
                 {'no surfacing': {0: 'no', 1: {'flippers': \
                                               {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
                 ]
    return listOfTrees[i]
1
2
3
myDat, labels = createDataSet()
myTree = retrieveTree(0)
classify(myTree, labels, [1, 0])
'no'
1
classify(myTree, labels, [1, 1])
'yes'

使用算法

构造决策树十分耗时，解决方案是把决策树存在磁盘中，使用时调用即可。

1
2
3
4
5
6
7
8
9
10
def storeTree(inputTree, filename):
    import pickle
    fw = open(filename, 'wb')
    pickle.dump(inputTree, fw)
    fw.close()
    
def grabTree(filename):
    import pickle
    fr = open(filename,'rb')
    return pickle.load(fr)
1
2
storeTree(myTree, 'classifier_dt.txt')
grabTree('classifier_dt.txt')
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
1
myTree
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

实例：预测隐形眼镜类型

1
2
3
4
fr = open('lenses.txt')
lenses = [inst.strip().split('\t') for inst in fr.readlines()]
lensesLabels = ['age', 'prescript', 'astigmatic', 'tearRate']
lensesTree = createTree(lenses, lensesLabels)
1
lensesTree
{'tearRate': {'normal': {'astigmatic': {'no': {'age': {'pre': 'soft',
      'presbyopic': {'prescript': {'hyper': 'soft', 'myope': 'no lenses'}},
      'young': 'soft'}},
    'yes': {'prescript': {'hyper': {'age': {'pre': 'no lenses',
        'presbyopic': 'no lenses',
        'young': 'hard'}},
      'myope': 'hard'}}}},
  'reduced': 'no lenses'}}
1
createPlot(lensesTree)
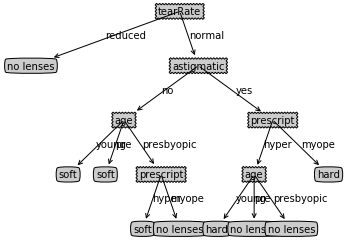
构建的决策树

构建的决策树

结论及讨论

结论

优点：计算复杂度不高，输出结果容易理解，对中间值缺失不敏感，可以处理不相关特征数据
缺点：可能会产生过拟合，此时需要裁剪决策树

讨论

  1. 对过拟合问题，可以采用剪枝，包括预剪枝和后剪枝。预剪枝是指在决策树生成过程中，对每个节点在划分前后进行估计，若当前节点的划分不能带来决策树泛化性能提升，则停止划分，并将当前节点记为叶节点；后剪枝则是先从训练集生成一颗完整的决策树，然后自底而上地对非叶节点进行考察，若将该节点对应的子树替换为叶节点也能带来决策树泛化性能提升，则将该子树替换为叶节点。
  2. 对连续属性，最简单的策略是采用二分法进行处理。对不同的候选划分点，采用和属性优选相同的策略，选出最优的划分点对该连续属性进行划分。
  3. 缺失值处理，需要回答两个问题：（1）如何选择属性？（2）给定划分属性，如何划分？首先对根节点的各个样本设置权值为1，在构建决策树的过程中，更新各个样本的权值。问题（1）的解决方案是对无缺失值的样本集计算信息增益，然后乘以无缺失值所占的比例，得到修正后的信息增益，再根据信息增益最大化选择属性；对于问题（2），如果样本在划分属性上的值已知，则将该样本划入与该值对应的子节点，并保持该样本的样本权值，如果样本在划分属性上值未知，则将该样本划入所有的子节点，但是该样本的样本权值调整为原来的权值乘以无缺失样本占该属性上取某值的样本所占的比例，这样就让同一个（缺失值）样本以不同的概率划入到不同的子节点中去。
  4. 多变量决策树，前面讨论的决策树形成的分类边界有一个明显的特征：轴平行，当学习任务的真实分类边界比较复杂时，必须使用很多段划分才能得到较好的近似，此时的决策树会相当复杂。原来的非叶节点是针对某个属性划分，改成对属性的线性组合进行测试，从而使得学习过程从对每个非叶节点寻找最优属性，变为建立一个合适的线性分类器。

参考资料

  1. Peter Harrington, Machine learning in action, Manning Publications, 2012
  2. 周志华，机器学习，清华大学出版社， 2016