AdaBoost算法是一种串行化的集成学习算法。其工作机制是:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个学习期,如此反复进行,直到基学习器数目达到实现制定的个数\(T\),最终将这\(T\)个基学习器进行加权结合,得到最终的预测结果。本文首先介绍AdaBoost算法的工作原理,然后介绍MLiA一书中该算法的实现以及该算法在马疝病的应用,最后介绍针对不平衡问题学习器的一些评估指标,包括查准率、查全率、AUC、代价敏感错误率、\(F1\)、\(PR\)曲线、\(ROC\)曲线、代价曲线等,以及对样本集的改造方法。
基本原理及算法
算法
算法工作流程: 1. 对训练集每个样本赋予一个权重\(D\),初始化为\(1/m\) 2. 根据训练集训练一个弱分类器,并计算该分类器的错误率: \[ \epsilon = \frac{m_w}{m} \] 其中\(m_w\)表示分类错误的样本数,\(m\)表示所有样本数。 3. 利用相同的训练集,但是调整每个样本的权重,再次训练一个弱分类器。 4. 为每个弱分类器分配一个权重值\(\alpha\) \[ \alpha = \frac{1}{2}log \left( \frac{1-\epsilon}{\epsilon} \right) \] 样本权重向量的更新公式为: 当样本分类正确, \[ D_i^{t+1} = \frac{D_i^t e^{-\alpha}}{\sum D} \] 当样本分类错误, \[ D_i^{t+1} = \frac{D_i^t e^{\alpha}}{\sum D} \] 5. 计算出权值后,进行下一次迭代。 6. 最终对弱分类器结果加权求和后得到最终预测的分类。
1 | from numpy import * |
1 | dataMat, classLabels = loadSimpData() |
png
1 | def stumpClassify(dataMatrix, dimen, threshVal, threshIneq): |
1 | D = mat(ones((5, 1))/5) |
({'dim': 0, 'ineq': 'lt', 'thresh': 1.3}, matrix([[ 0.2]]), array([[-1.],
[ 1.],
[-1.],
[-1.],
[ 1.]]))1 | def adaBoostTrainDS(dataArr, classLabels, numIt=40): |
1 | classifierArray = adaBoostTrainDS(dataMat, classLabels, 9) |
total error: 0.2
total error: 0.2
total error: 0.0 1 | classifierArray |
[{'alpha': 0.6931471805599453, 'dim': 0, 'ineq': 'lt', 'thresh': 1.3},
{'alpha': 0.9729550745276565, 'dim': 1, 'ineq': 'lt', 'thresh': 1.0},
{'alpha': 0.8958797346140273,
'dim': 0,
'ineq': 'lt',
'thresh': 0.90000000000000002}]测试算法
1 | def adaClassify(dataToClass, classifierArr): |
1 | adaClassify([0, 0], classifierArray) |
matrix([[-1.]])实例1:马疝病预测
1 | def loadDataSet(fileName): |
1 | dataArr, labelArr = loadDataSet('horseColicTraining2.txt') |
total error: 0.284280936455 1 | testArr, testLabelArr = loadDataSet('horseColicTest2.txt') |
0.26865671641791045| 分类器数目 | train error(%) | test error(%) |
|---|---|---|
| 1 | 28.4 | 26.9 |
| 10 | 23.1 | 23.8 |
| 50 | 18.7 | 20.8 |
| 100 | 19.1 | 22.4 |
| 200 | 16.7 | 22.4 |
| 500 | 15.7 | 25.4 |
非均衡分类问题
查准率、查全率与F1
查准率(Precision)定义为真正例占预测为正例的比例: \[ P = \frac{TP}{TP+FP} \] 查全率(Recall)定义为真正例占所有真实正例的比例: \[ R = \frac{TP}{TP+FN} \]
混淆矩阵
| 预测为正例 | 预测为反例 | |
|---|---|---|
| 正例 | 真正例(TP) | 假反例(FN) |
| 反例 | 假正例(FP) | 真反例(TN) |
如果学习器的输出是一个实数或者概率预测,根据预测结果对样例进行排序,按此顺序逐个把样本作为正例进行预测,每次计算查准率和查全率,并作为纵、横轴,就得到查准率-查全率曲线,简称P-R曲线。
若果一个学习器被另一个学习器完全“包住”,则可以断言后者的性能优于前者;如果两个学习器的ROC曲线发生交叉,则很难一般性地断言两者哪个更优。如果一定要比较,较为合理的判据是比较P-R曲线下的面积,但是这个值不太容易估计,更常用的是F1度量: \[ F1 = \frac{2*P*R}{P+R} \] 实际上,\(F1\)是查准率和查全率的调和平均值: \[ \frac{1}{F1} = \frac{1}{2} \left( \frac{1}{P}+\frac{1}{R} \right) \] 与算术平均\(\frac{P+R}{2}\)和几何平均\(\sqrt{(P*R)}\)相比,调和平均更加注重小值。
在不同的应用中,往往对查准率和查全率重视程度不同,例如犯罪信息检查,重视查全率,商品推荐,重视查准率。为此,有比\(F1\)的更一般化的\(F_{\beta}\)度量,定义为: \[ F_{\beta} = \frac{(1+\beta^2)*P*R}{\beta^2*P+R} \] 类似的,\(F_{\beta}\)是查准率和查全率的加权调和平均值: \[ \frac{1}{F1} = \frac{1}{1+\beta^2} \left( \frac{1}{P}+\frac{\beta^2}{R} \right) \] 其中\(\beta>0\)度量了查全率对查准率的相对重要性,\(\beta>1\)查全率影响更大,\(\beta<1\)查准率更重要。
最后一个问题,当多次训练/测试,每次得到一个混淆矩阵,为了计算\(F_\beta\),一种办法是对\(P\)和\(R\)平均,另一种办法是对\(TP,FP,TN,FN\)平均,结果分别叫宏\(F_\beta\)和微\(F_\beta\)。
ROC与AUC
ROC(Receiver Operating Characteristic)受试者工作特征曲线,根据预测结果对样例进行排序,按此顺序逐个把样本作为正例进行预测,每次计算真正例率(TPR:表示真正例占真实正例的比例)和假正例率(FPR:表示假正例占真实反例的比例),并作为纵、横轴数值。 \[ TPR = \frac{TP}{TP+FN} \] \[ FPR = \frac{FP}{FP+TN} \] 从ROC的定义可以看出,对角线对应于“随机猜测”模型,而点(0,1)则对应于将偶有的正例都排在所有反例之前的“理想模型”。
若果一个学习器被另一个学习器完全“包住”,则可以断言后者的性能优于前者;如果两个学习器的ROC曲线发生交叉,则很难一般性地断言两者哪个更优。如果一定要比较,较为合理的判据是比较ROC曲线下的面积,即AUC(Area Under ROC Curve)。
1 | def plotROC(predStrengths, classLabels): |
1 | dataArr, labelArr = loadDataSet('horseColicTraining2.txt') |
total error: 0.284280936455
total error: 0.284280936455
total error: 0.247491638796
total error: 0.247491638796
total error: 0.254180602007
total error: 0.240802675585
total error: 0.240802675585
total error: 0.220735785953
total error: 0.247491638796
total error: 0.230769230769 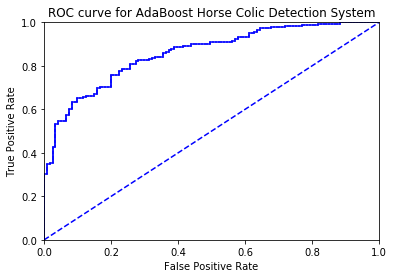
png
the area under the curve is: 0.8582969635063604代价敏感错误率与代价曲线
把病人诊断为患者,和把患者诊断为健康人,两种错误造成的损失是不同的,因此可以为其赋予非均等代价,
代价矩阵
| 预测为正例 | 预测为反例 | |
|---|---|---|
| 正例 | 0 | \(cost_{01}\) |
| 反例 | \(cost_{10}\) | 0 |
代价敏感(cost-sensitive)错误率定义为: \[ E(f; D; cost) = \frac{1}{m} \sum_{\mathbf{x}_i \in D^+} I(f(\mathbf{x}_i) \neq y_i) cost_{01} + \sum_{\mathbf{x}_i \in D^-} I(f(\mathbf{x}_i) \neq y_i) cost_{10} \]
ROC曲线不能直接反映学习器的期望总体代价,代价曲线(cost curve)则可以达到目的。代价曲线的横轴是取值\([0,1]\)的正例概率代价: \[ P(+)cost = \frac{p*cost_{01}}{p*cost_{01}+(1-p)*cost_{10}} \] 其中\(p\)是样例为正例的概率;纵轴是取值为\([0,1]\)的归一化代价: \[ cost_{norm} = \frac{FNR*p*cost_{01}+FPR×(1-p)*cost_{10}}{p*cost_{01}+(1-p)*cost_{10}} \] 其中\(FPR\)是假正例率,\(FNR = 1 - TPR\)表示假反例率。
代价函数的绘制很简单:ROC上的每一个点对应代价平面上的一条线段,假设ROC曲线上点的坐标\((FPR, TPR)\),则可以相应的计算\(FNR\),然后在代价平面上绘制一条从\((0, FPR*cost_{10})\)到\((1, FNR*cost_{01})\)的线段,线段下的面积表示了该条件下的期望总体代价;如此将ROC曲线上的每个点都转化成代价平面上的一个线段,然后取所有线段的下界,围成的面积就是在所有条件下学习器的期望总体代价。
处理非均衡问题的数据抽样方法
另外一种针对非均衡数据问题调节分类器的方法,是对训练数据进行改造,可以通过欠抽样或者过抽样来实现。比如信用卡欺诈中,正例很少,反例很多,一种解决方案是删除那些离决策边界较远的样例。另一种策略是使用反例类别的欠抽样和正例类别的过抽样相混合。但是需要注意的是,复制已有样例或者加入与已有样例相似的特点,或者加入已有数据点的插值点,都可能会导致过拟合。
结论及讨论
结论
AdaBoost集成学习具有以下特点: > - 优点:泛化错误率低,容易编码,可以应用在大部分分类器上,无参数调整(唯一的参数是串联多少个分类器) > - 缺点:对离群点敏感
讨论
- 本文只讨论了集成学习中的串联集成方式,还有一种并行集成方式,其代表算法是随机森林。
- 本文值只讨论了“重赋权法”对调整样本数据,对无法接受带权样本的基学习器不适用,还有一种重采样方法,可以根据样本分布对训练集进行重采样。
- 对分类器的度量指标有很多,并不是一件简单的事情。
- 处理非均衡问题,除了需要设计合理的度量指标外,还需要对样本集进行改造。
参考资料
- Peter Harrington, Machine learning in action, Manning Publications, 2012
- 周志华,机器学习,清华大学出版社, 2016

