树回归 | Home of a Explorer

本文主要介绍两种树形结构用于求解回归问题：一种是回归树，叶节点用均值，误差用总方差衡量；另一种是模型树，叶节点为线性回归模型，误差用线性回归误差衡量。对样本集进行二分后，计算二分后误差有没有改善，如果没有，则停止二分；如果有改善，则继续进行二分。但是，如果节点过多，模型可能对数据过拟合，此时可以采用树剪枝处理，包括预剪枝和后剪枝。最后介绍MLiA一书中使用tkinter编写GUI交互调试树回归参数。

基本原理及算法

回归树

CART(Classification and Regression Trees)算法是树回归中十分著名的树构建算法。其思想和ID3算法类似，不同之处在于，数据划分采用二分方式，是否划分是根据总方差是否减少来决定，叶节点是数据集\(y\)的均值（数值型）。

class treeNode():
    def __init__(self, feat, val, right, left):
        featureToSplitOn = feat
        valueOfSplit = val
        rightBranch = right
        leftBranch = left

from numpy import *

def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float, curLine))
        dataMat.append(fltLine)
    return dataMat

def binSplitDataSet(dataSet, feature, value):
    """
    根据特征值划分数据集
    dataSet: 输入数据集 (m, n)
    feature: 数据集划分所根据的特征
    value: 划分的界限
    """
    mat0 = dataSet[nonzero(dataSet[:,feature] > value)[0], :] # 提取特征值大于value的样本
    mat1 = dataSet[nonzero(dataSet[:,feature] <= value)[0], :]
    return mat0, mat1

testMat = mat(eye(4))
mat0, mat1 = binSplitDataSet(testMat, 1, 0.5)
print(mat0)
print(mat1)

[[ 0.  1.  0.  0.]]
[[ 1.  0.  0.  0.]
 [ 0.  0.  1.  0.]
 [ 0.  0.  0.  1.]]

1	nonzero(testMat[:,1]<=0.5)

(array([0, 2, 3]), array([0, 0, 0]))

def regLeaf(dataSet):
    """
    叶节点，直接返回真实的y值平方
    """
    return mean(dataSet[:, -1])

def regErr(dataSet):
    """
    计算真实y值的总方差，以估计连续数据值的混乱程度
    """
    return var(dataSet[:, -1]) * shape(dataSet)[0] # 真实y的总方差：均方差×样本数

def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1, 4)):
    """
    dataSet: (m, n)
    ops[0]: 容许的误差值
    ops[1]: 切分的最小样本数
    """
    tolS = ops[0]; tolN = ops[1]
    if len(set(dataSet[:,-1].T.tolist()[0])) == 1: # y值的个数，如果都相等，则退出
        return None, leafType(dataSet)
    m, n = shape(dataSet)
    S = errType(dataSet) # 计算y值的总方差
    bestS = inf; bestIndex = 0; bestValue = 0
    
    # 遍历所有的特征
    for featIndex in range(n-1):
        # 遍历该特征所有可能的取值
        for splitVal in set(dataSet[:, featIndex].T.A.tolist()[0]):
            # 利用该特征的特定取值对数据集进行划分
            mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
            # 如果划分后的数据集样本个数少于设置的切分样本最小个数，则直接进行下一次循环
            if (mat0.shape[0] < tolN) or (mat1.shape[0] < tolN): continue
            # 计算划分后两个样本集的总方差
            newS = errType(mat0) + errType(mat1)
            # 寻找最小总方差对应的特征及划分值
            if newS < bestS:
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
                
    # 如果和原来的数据集误差差别不打，则直接创建叶节点。
    if (S - bestS) < tolS:
        return None, leafType(dataSet)
    
    # 根据前面的搜索结果划分数据集
    mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
    
    # 如果划分后的数据集小于设定的最小样本数，则直接创建叶节点
    if (mat0.shape[0] < tolN) or (mat1.shape[0] < tolN):
        return None, leafType(dataSet)
    
    return bestIndex, bestValue

def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
    feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
    if feat == None: return val
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    lSet, rSet = binSplitDataSet(dataSet, feat, val)
    retTree['left'] = createTree(lSet, leafType, errType, ops)
    retTree['right'] = createTree(rSet, leafType, errType, ops)
    return retTree

1
2
3

myDat = loadDataSet('ex00.txt')
myMat = mat(myDat)
createTree(myMat)

{'left': 1.0180967672413792,
 'right': -0.044650285714285719,
 'spInd': 0,
 'spVal': 0.48813}

1
2
3

myDat1 = loadDataSet('ex2.txt')
myMat1 = mat(myDat1)
myTree1 = createTree(myMat1)

树剪枝

剪枝（pruning）是决策树学习算法对付“过拟合”的主要手段。其基本策略包括预剪枝（prepruning）和后剪枝（postpruning），预剪枝是指在决策树生成过程中，对每个节点在划分前后进行估计，若果当前节点的划分不能带来泛化性能的提升，则停止划分，并将当前节点标记为叶节点；后剪枝则是先从训练集生成一颗完整的决策树，然后自底而上对非叶节点进行考察，若将该节点对应的子树替换为叶节点能带来泛化性能的提升，则将该子树替换为叶节点。

预剪枝

1	createTree(myMat, ops=(0,1))

1
2
3

myDat2 = loadDataSet('ex3.txt')
myMat2 = mat(myDat2)
createTree(myMat2)

1	createTree(myMat2,ops=(10000,4))

{'left': 101.35815937735848,
 'right': -2.6377193297872341,
 'spInd': 0,
 'spVal': 0.499171}

后剪枝

def isTree(obj):
    """
    判断是否是一棵树
    """
    return (type(obj).__name__=='dict')

def getMean(tree):
    """
    递归地从上往下遍历树直到叶节点为止，如果找到两个叶节点，则计算它们的平均值
    """
    if isTree(tree['right']): tree['right'] = getMean(tree['right'])
    if isTree(tree['left']): tree['left'] = getMean(tree['left'])
    return (tree['left']+tree['right'])/2.0
    
def prune(tree, testData):
    """
    后剪枝
    """
    if shape(testData)[0] == 0: return getMean(tree) #没有测试数据，则使用构建的树作平均
    
    # 先根据树信息对测试数据划分
    if isTree(tree['right']) or isTree(tree['left']):
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
        
    # 如果是子树，则递归调用prune进行剪枝
    if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet)
    if isTree(tree['right']): tree['right'] = prune(tree['right'], rSet)
        
    # 如果不是子树，而是叶节点，则进行合并测试
    if not isTree(tree['right']) and not isTree(tree['left']):
        # 现对测试数据进行划分
        lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
        # 计算合并前的误差
        errorNoMerge = sum(power(lSet[:-1] - tree['left'], 2)) + \
                       sum(power(rSet[:-1] - tree['right'], 2))
        # 合并后计算误差
        treeMean = (tree['left'] + tree['right'])/2.0
        errorMerge = sum(power(testData[:,-1] - treeMean, 2))
        
        # 如果合并后的误差小于合并前的误差，则进行合并
        if errorMerge < errorNoMerge:
            print ("merging")
            return treeMean
        else: return tree
    else: return tree

myTree = createTree(myMat2, ops=(0, 1))
#getMean(myTree)
myDatTest = loadDataSet('ex2test.txt')
myMatTest = mat(myDatTest)
#prune(myTree, myMatTest)

模型树

def linearSolve(dataSet):
    m, n = shape(dataSet)
    X = mat(ones((m, n))); Y = mat(ones((m, 1)))
    X[:, 1:n] = dataSet[:, 0:n-1]; Y = dataSet[:, -1] # 将第一个feature设置为常数１
    xTx = X.T*X
    if linalg.det(xTx) == 0.0:
        raise NameError('this matrix is singular, try increasing the second value of ops')
    ws = xTx.I * (X.T * Y)
    return ws, X, Y

def modelLeaf(dataSet):
    ws, X, Y = linearSolve(dataSet)
    return ws

def modelErr(dataSet):
    ws, X, Y = linearSolve(dataSet)
    yHat = X * ws
    return sum(power(Y-yHat, 2))

1 2	myMat2 = mat(loadDataSet('exp2.txt')) createTree(myMat2, modelLeaf, modelErr, (1, 10))

{'left': matrix([[  1.69855694e-03],
         [  1.19647739e+01]]), 'right': matrix([[ 3.46877936],
         [ 1.18521743]]), 'spInd': 0, 'spVal': 0.285477}

后剪枝往往比预剪枝保留更多的分支，欠拟合风险更小，泛化性能往往优于预剪枝决策树。但是后剪枝是在生成完全决策树之后进行的，而且要自底而上对树中的所有非叶节点进行逐一考察，因此其训练开销比未剪枝和预剪枝决策树要大得多。

对比树回归与标准回归

def regTreeEval(model, inDat):
    """
    回归树预测
    model：叶节点是样本集合y的均值
    """
    return float(model)

def modelTreeEval(model, inDat):
    """
    模型树预测
    model：叶节点是线性模型的权系数
    inDat：输入样本集(m, n)
    """
    n = shape(inDat)[1]
    X = mat(ones((1, n+1)))
    X[:, 1:n+1] = inDat
    return float(X*model)

def treeForeCast(tree, inDat, modelEval=regTreeEval):
    """
    预测单个样点的回归值
    tree：训练得到的树模型
    inDat: 输入的一个样点(n, 1)
    modelEval：模型预测方法，有回归树和模型树两种
    """
    # 如果不是树结构，意味着只有只有一个节点，直接调用模型预测
    if not isTree(tree): return modelEval(tree, inDat)
    
    # 如果样点位于划分阈值的左侧
    if inDat[tree['spInd']] > tree['spVal']:
        # 如果是子树节点，继续递归调用
        if isTree(tree['left']):
            return treeForeCast(tree['left'], inDat, modelEval)
        # 如果是叶节点，调用模型预测
        else:
            return modelEval(tree['left'], inDat)
    else:
        if isTree(tree['right']):
            return treeForeCast(tree['right'], inDat, modelEval)
        else:
            return modelEval(tree['right'], inDat)
        
def createForeCast(tree, testData, modelEval=regTreeEval):
    """
    预测所有测试数据的回归值
    tree：训练得到的树模型
    testData：测试数据
    modelEval：模型预测方法，有回归树和模型树两种
    """
    m = len(testData)
    yHat = mat(zeros((m, 1)))
    for i in range(m):
        yHat[i, 0] = treeForeCast(tree, mat(testData[i]), modelEval)
    return yHat

#　回归树
trainMat = mat(loadDataSet('bikeSpeedVsIq_train.txt'))
testMat = mat(loadDataSet('bikeSpeedVsIq_test.txt'))
myTree = createTree(trainMat, ops=(1,20))
yHat = createForeCast(myTree, testMat[:,0])

#利用相关系数评估预测结果
corrcoef(yHat, testMat[:,1], rowvar=0)[0, 1]

0.96408523182221451

# 模型树
myTree = createTree(trainMat, modelLeaf, modelErr, ops=(1,20))
yHat = createForeCast(myTree, testMat[:,0], modelTreeEval)
# 利用相关系数评估预测结果
corrcoef(yHat, testMat[:,1], rowvar=0)[0, 1]

0.9760412191380623

# 标准的线性回归
ws, X, Y = linearSolve(trainMat)
for i in range(shape(testMat)[0]):
    yHat[i] = testMat[i,0]*ws[1, 0] + ws[0, 0]
corrcoef(yHat, testMat[:,1], rowvar=0)[0, 1]

0.94346842356747618

图形交互

1
2
3

from tkinter import *
root = Tk()
root.mainloop()

from numpy import *
from tkinter import *

import matplotlib
matplotlib.use('TkAgg')
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
from matplotlib.figure import Figure

def reDraw(tolS, tolN):
    reDraw.f.clf() # 清空原来的图像
    reDraw.a = reDraw.f.add_subplot(111) # 增加一个图像
    
    # 复选框是否被选中
    if chkBtnVar.get():
        if tolN < 2: tolN = 2
        myTree = createTree(reDraw.rawDat, modelLeaf, modelErr, (tolS, tolN))
        yHat = createForeCast(myTree, reDraw.testDat, modelTreeEval)
    else:
        myTree = createTree(reDraw.rawDat, ops=(tolS, tolN))
        yHat = createForeCast(myTree, reDraw.testDat)
        
    reDraw.a.scatter(reDraw.rawDat[:,0].tolist(), reDraw.rawDat[:,1].tolist(), s=5)
    reDraw.a.plot(reDraw.testDat, yHat, linewidth=2.0)
    reDraw.canvas.show()

def getInputs():
    try: tolN = int(tolNentry.get())
    except:
        tolN = 10
        print ("enter integer for tolN")
        tolNentry.delete(0, END)
        tolNentry.insert(0, '10')
    try: tolS = int(tolSentry.get())
    except:
        tolS = 1.0
        print("enter float for tolS")
        tolSentry.delete(0, END)
        tolSentry.insert(0, '1.0')
    return tolN, tolS

def drawNewTree():
    tolN, tolS = getInputs()
    reDraw(tolS, tolN)

# 创建Tk类的根部件
root = Tk()

#Label(root, text="Plot Place Holder").grid(row=0, columnspan=3)
reDraw.f = Figure(figsize=(5, 4), dpi=100)
reDraw.canvas = FigureCanvasTkAgg(reDraw.f, master=root)
reDraw.canvas.show()
reDraw.canvas.get_tk_widget().grid(row=0, columnspan=3)

# 插入一个文本框
Label(root, text="tolN").grid(row=1, column=0)
tolNentry = Entry(root)
tolNentry.grid(row=1, column=1)
tolNentry.insert(0, '10')

# 插入一个文本框
Label(root, text="tolS").grid(row=2, column=0)
tolSentry = Entry(root)
tolSentry.grid(row=2, column=1)
tolSentry.insert(0, '1.0')

# 插入一个按钮
Button(root, text="ReDraw", command=drawNewTree).grid(row=1, column=2, rowspan=3)

# 插入一个复选框
chkBtnVar = IntVar()
chkBtn = Checkbutton(root, text="Model Tree", variable = chkBtnVar)
chkBtn.grid(row=3, column=0, columnspan=2)

reDraw.rawDat = mat(loadDataSet('sine.txt'))
reDraw.testDat = arange(min(reDraw.rawDat[:,0]), max(reDraw.rawDat[:,0]), 0.01)
reDraw(1.0, 10)

root.mainloop()

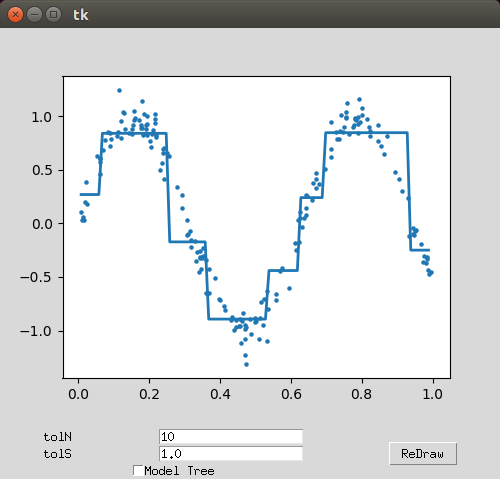
树回归

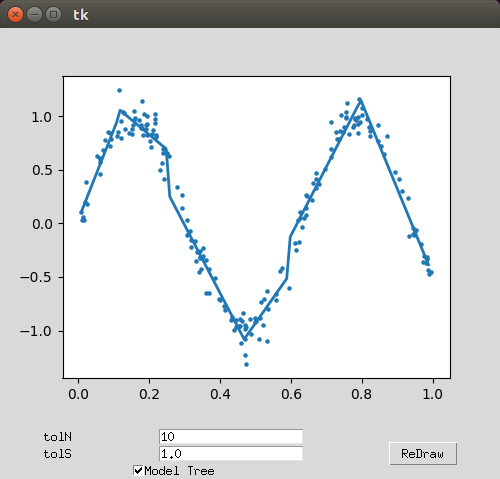
模型回归

结论及讨论

结论

树回归具有以下特点： > - 优点：可以对复杂和非线性数据进行建模 > - 缺点：结果不易理解

讨论

树回归和决策树中的叶节点上可以嵌入神经网络，如感知机树，甚至嵌入深度神经网络。
利用树结构进行增量学习，即在接受到新样本后对已学得的模型进行调整，而不用完全重新学习。其主要机制是通过调整分支路径上的划分属性次序对树进行部分重构，代表算法有ID4,ID5R等。

参考资料

Peter Harrington, Machine learning in action, Manning Publications, 2012
周志华，机器学习，清华大学出版社， 2016