K-均值

发表于 | 分类于

K-均值算法是无监督学习中的经典算法，该方法的基本思想是“物以类聚”，将相似的样本归到同一个簇中。算法分两步实现，第一步对样本点分配簇标记，第二部更新簇中心坐标。该算法受初始值的影响较大，容易陷入局部极值，一种做法是不断对簇进行二分，直到满足用户设定的最大簇数目为止。本文除了介绍K-均值算法的基本原理及算法外，也详细讲解MLiA一书中的程序实现。

基本原理及算法

基本原理

K-均值方法最小化以下目标函数: \[ J(c^{(1)}, ..., c^{(m)}; \mu_1, ..., \mu_k) = \frac{1}{m} \sum_{i=1}^{m} \| \mathbf{x}^{(i)} - \mu_{c^{(i)}} \|^2 \] 其中：
\(c^{(i)}\)表示样本\(\mathbf{x}^{(i)}\)的簇标记，\(i=1,2,...,m\)
\(\mu_k\)表示第\(k\)簇的中心坐标，\(\mu_k \in \mathbb{R}^n\)
\(\mu_{c^{(i)}}\)表示样本\(\mathbf{x}^{(i)}\)分配到的簇所对应的中心点坐标。

K-均值算法

算法实现过程如下： > 1. 初始化所有k簇的中心坐标（两种方式，一种是随机从样点中拾取k个样点作为簇中心坐标；另一种是在特征值范围内随机生成数值作为簇中心坐标，本文采用第二种方法）
> 2. 根据每个样点和簇中心的距离，将每个样点分配不同的簇 > 3. 对每个簇内的样本取平均值，更新簇中心的坐标 > 4. 重复第2，第3步，直到簇的分配结果不发生变化为止

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from numpy import *

def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float, curLine))
        dataMat.append(fltLine)
    return dataMat

def distEclud(vecA, vecB):
    """计算两个向量的欧氏距离"""
    return sqrt(sum(power(vecA - vecB, 2)))

def randCent(dataSet, k):
    """
    随机方式初始化中心点坐标
    """
    n = shape(dataSet)[1]
    centroids = mat(zeros((k, n)))
    for j in range(n):
        minJ = min(dataSet[:, j])
        rangeJ = float(max(dataSet[:, j]) - minJ) # 第j个特征的范围
        centroids[:, j] = minJ + rangeJ * random.rand(k, 1) # 随机产生k个给定范围内的随机数
    return centroids
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def kMeans(dataSet, k, distMeans=distEclud, createCent=randCent):
    m = shape(dataSet)[0] #数据样本个数
    clusterAssment = mat(zeros((m, 2))) # 存储簇分配结果，第一列存簇的索引，第二类存误差
    centroids = createCent(dataSet, k)
    clusterChanged = True
    
    # 只要有样点所属的簇发生变化，继续迭代
    while clusterChanged:
        clusterChanged = False
        # 样点循环
        for i in range(m):
            minDist = inf; minIndex = -1
            # 簇循环
            for j in range(k):
                # 计算簇中心和样点之间的距离
                distJI = distMeans(centroids[j,:], dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI; minIndex = j
                    
            if clusterAssment[i,0] != minIndex:
                clusterChanged = True
            # 将簇所对应的索引以及簇中心和样点之间的距离存储下来
            clusterAssment[i,:] = minIndex, minDist**2
        print(centroids)
        
        # 更新簇中心的坐标
        for cent in range(k):
            # 提取所有属于第cent簇的样本索引
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]
            # 计算所有样点的中点坐标，作为最新的簇中心坐标
            centroids[cent,:] = mean(ptsInClust, axis=0)
            
    return centroids, clusterAssment
1
2
dataMat = mat(loadDataSet('testSet3.txt'))
myCentroids, clusterAssing = kMeans(dataMat, 4)
[[ 0.31932261  2.73155484]
 [ 0.37875077 -1.20000209]
 [ 4.03208021  0.41923412]
 [ 0.12274597 -1.40061489]]
[[-0.52674659  3.20699566]
 [ 2.5935345  -2.92880329]
 [ 3.74487682  0.74644273]
 [-2.99723017 -2.84727778]]
[[-1.4837585   3.05005908]
 [ 2.60265739 -2.92536139]
 [ 3.193015    2.29036194]
 [-3.38237045 -2.9473363 ]]
[[-2.46154315  2.78737555]
 [ 2.80293085 -2.7315146 ]
 [ 2.6265299   3.10868015]
 [-3.38237045 -2.9473363 ]]

二分K-均值算法

为了客服K-均值算法收敛于局部极小值，一种方法是二分K-均值算法。该算法首先将所有的点划为一簇，然后将簇一分为二。之后再选择其中一个簇继续进行划分。选择哪一个簇划分取决于划分后能否最大程度上降低误差平方和。上述划分过程不断重复，直到用户指定的簇数目位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
def biKmeans(dataSet, k, distMeas=distEclud):
    """
    dataSet: 输入样本集
    k: 聚类数目
    distMeas: 距离计算方法
    """
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m, 2))) # 存储每个样点的簇类分配结果及平方误差
    centroid0 = mean(dataSet, axis=0).tolist()[0]
    centList = [centroid0] # 簇中心
    
    # 计算每个样点和簇中心的误差
    for j in range(m):
        clusterAssment[j, 1] = distMeas(mat(centroid0), dataSet[j, :])**2
    
    while (len(centList) < k):
        lowestSSE = inf
        
        # 遍历所有簇，找到最需要二分的簇
        for i in range(len(centList)):
            # 属于第i个簇的样本集合
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:, 0].A == i)[0], :]
            # 将该样本集使用k-means方法进行二分
            centroidMat, splitClusterAss = kMeans(ptsInCurrCluster, 2, distMeas)
            # 得到二分后的总误差
            sseSplit = sum(splitClusterAss[:, 1])
            # 不属于第i个簇的剩余样本集合的总误差
            sseNoSplit = sum(clusterAssment[nonzero(clusterAssment[:, 0].A != i)[0], 1])
            print("sseSplit, and notSplit: ", sseSplit, sseNoSplit)
            # 判断二分后的总误差和剩余样本集合的总误差是否比原来更小，如果是，则保存本次划分结果
            if (sseSplit + sseNoSplit) < lowestSSE:
                bestCentToSplit = i # 将要划分的簇
                bestNewCents = centroidMat #新的簇中心
                bestClustAss = splitClusterAss.copy() #样本集合新的簇标记
                lowestSSE = sseSplit + sseNoSplit #更新后的总误差
        
        # 将二分簇编号(0,1)修改为新簇的编号
        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) # 修改簇标记,新增的部分
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit # 修改簇标记，留下的部分
        print("the bestCentToSplit is: ", bestCentToSplit)
        print("the len of bestClustAss is: ", len(bestClustAss))
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0] # 修改簇中心坐标
        centList.append(bestNewCents[1, :].tolist()[0]) #　添加簇中心坐标
        clusterAssment[nonzero(clusterAssment[:,0].A==bestCentToSplit)[0],:] = bestClustAss # 对样本分配新的簇标记
    return mat(centList), clusterAssment
1
2
dataMat3 = mat(loadDataSet('testSet5.txt'))
centList, myNewAssments = biKmeans(dataMat3, 3)
[[ 3.16802386 -0.45393748]
 [ 0.56338737 -1.59314948]]
[[ 2.93386365  3.12782785]
 [-1.70351595  0.27408125]]
sseSplit, and notSplit:  541.297629265 0.0
the bestCentToSplit is:  0
the len of bestClustAss is:  60
[[ 4.58031512  4.72206728]
 [ 4.04178843  1.45919552]]
[[ 3.26127644  3.86529411]
 [ 2.66598045  2.52444636]]
[[ 3.43738162  3.905037  ]
 [ 2.598185    2.60968842]]
sseSplit, and notSplit:  28.0948398289 501.768330583
[[-2.77258829  4.28278805]
 [ 0.24829799 -0.23792833]]
[[-2.94737575  3.3263781 ]
 [-0.45965615 -2.7782156 ]]
sseSplit, and notSplit:  67.2202000798 39.5292986821
the bestCentToSplit is:  1
the len of bestClustAss is:  40
1
centList
matrix([[ 2.93386365,  3.12782785],
        [-2.94737575,  3.3263781 ],
        [-0.45965615, -2.7782156 ]])
1
2
3
4
5
6
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat3[:,0].A, dataMat3[:,1].A, s=50, c='red')
ax.scatter(centList[:,0].A, centList[:,1].A, s=100,c='blue')
plt.show()
png

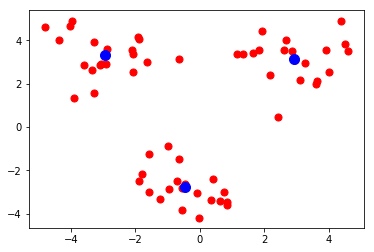
png

1
centList0, myNewAssments0 = kMeans(dataMat3, 3)
[[ 0.71500846 -0.20160621]
 [ 4.2255342   3.75218205]
 [-4.43563586 -2.52571969]]
[[-1.29839539  0.32851418]
 [ 2.95977168  3.26903847]
 [-2.85649738  0.0708885 ]]
[[-0.67935225 -1.00546612]
 [ 2.93386365  3.12782785]
 [-3.2397615   2.19340231]]
[[-0.45965615 -2.7782156 ]
 [ 2.93386365  3.12782785]
 [-2.94737575  3.3263781 ]]
1
2
3
4
5
6
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat3[:,0].A, dataMat3[:,1].A, s=50, c='red')
ax.scatter(centList0[:,0].A, centList0[:,1].A, s=100,c='blue')
plt.show()
png

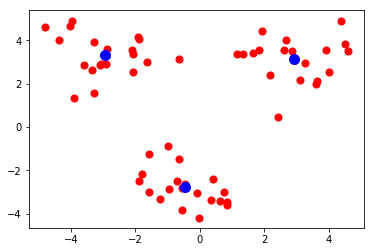
png

结论及讨论

结论

K-均值算法具有以下特点: > - 优点：容易实现 > - 缺点：可能收敛到局部极小值，在大规模数据集上收敛较慢

讨论

  1. K-均值算法的一种难点是k的选择，一种方法是监控总平方误差随k的变化曲线，选择曲线的拐点作为k的值。该方法称为Elbow方法。
  2. 聚类既能作为一个单独过程，用于寻找数据内在的分布结构，也可以作为分类等其他学习任务的前驱过程。