主成分分析

发表于 | 分类于

为了缓解高维情形下出现的数据样本稀疏、距离计算困难等问题，一个重要途径是降维。主成分分析（PCA）是应用最为广泛的一种降维技术。本文将介绍主成分分析的基本原理及算法实现。

基本原理及算法

基本原理

假定有\(m\)个样本，每个样本有\(n\)个属性，数据矩阵表述为\(X_{n \times m}\)。降维的目标是：在尽可能少地损失有效信息的前提下，减少属性的个数。假如采用矩阵\(M_{r \times n}\)将数据进行线性映射，得到数据\(Y_{r \times m}\), \[ Y_{r \times m} = M_{r \times n} X_{n \times m} \] 矩阵乘法的物理意义是将每个样点代表的\(n\)维向量投影到\(r\)维空间。如果\(r<n\)，则达到了降维的目的。为了使得降维后保留更多的信息，直观的看法是使得投影后的样本尽可能分散。为了描述分散程度，可以用数学上的方差来描述。假定数据已经消除均值（均值为0），则原数据方差为： \[ Cov(X) = \frac{1}{m} X X^T \] 协方差矩阵对角线元素描述的是样本在各属性上分布的方差，非对角线线元素描述的是不同属性之间的相关性。降维的目标是使得数据经投影后方差尽可能大，而属性之间正交，也就是使得\(Var(Y)\)为对角矩阵。 \[ Cov(Y) = \frac{1}{m} M X (M X)^T = M \left( \frac{1}{m} X X^T \right) M^T = M Cov(X) M^T \] 对角化可以采用特征值分解： \[ Cov(X) = E \Lambda E^{-1} \] 其中矩阵\(E\)为特征向量组成的矩阵，\(\Lambda\)为特征值为对角线元素组成的对角矩阵，令： \[ M = E^T \] 则， \[ Cov(Y) = \Lambda \] 由于\(Cov(X)\)是对称正定矩阵，奇异值分解和特征值分解相同： \[ Cov(X) = U \Sigma V^T \] 此时\(U=E\)，\(\Sigma=\Lambda\)。

为了达到降维的效果，特征值分解之后，取前\(r\)个最大的特征值对应的特征向量，每个特征向量作为矩阵\(M\)的行向量，再利用下面的公式即可以达到降维的目的： \[ Y_{r \times m} = M_{r \times n} X_{n \times m} \]

在实际应用中，也常常对原来的数据矩阵进行奇异值分解， \[ X = \hat{U} \hat{\Sigma} \hat{V}^T \] 则： \[ Cov(X) = \hat{U} \hat{\Sigma}^2 \hat{U}^T \] 令\(M = U^T\)，同样可以实现降维的目的。

算法实现

PCA算法实现分为以下几步：
1. 对数据进行零均值化处理，如果不同特征尺度相差较大，也需要进行方差归一化处理；
2. 对数据集的协方差矩阵进行特征值分解，或者直接对数据集进行特征值分解；
3. 选择最大的前\(r\)个特征值（或奇异值）对应的特征向量组成线性变换矩阵；
4. 应用变换矩阵对数据降维处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from numpy import *

def loadDataSet(fileName, delim='\t'):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    #print(stringArr)
    datArr = [list(map(float,line)) for line in stringArr]
    return mat(datArr)

def pca(dataMat, topNfeat=9999999):
    """
    主成分分析
    dataMat: (m, n)
    """
    meanVals = mean(dataMat, axis=0) # 取所有样本的均值
    meanRemoved = dataMat - meanVals # 减去均值
    covMat = cov(meanRemoved, rowvar=0) # 计算协方差，一列表示一个向量
    eigVals, eigVects = linalg.eig(mat(covMat)) # 特征值分解
    eigValInd = argsort(eigVals) # 对特征值对小到大排序
    eigValInd = eigValInd[:-(topNfeat+1):-1] # 逆序从最后一个到倒数第topNfeat个属性
    redEigVects = eigVects[:, eigValInd]
    lowDDataMat = meanRemoved * redEigVects
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    return lowDDataMat, reconMat
1
2
3
dataMat = loadDataSet('testSet6.txt')
lowDMat, reconMat = pca(dataMat, 1)
print(shape(dataMat),shape(lowDMat))
(1000, 2) (1000, 1)
1
2
3
4
5
6
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat[:,0].A, dataMat[:,1].A, marker='^', s=90)
ax.scatter(reconMat[:,0].A, reconMat[:,1].A, marker='o', s=50, c='red')
plt.show()
png

png

选择主成分的数量

计算前\(r\)个特征值的能量占总特征值能量的比例: \[ \frac{\sum_{i=1}^{r} \lambda_i}{\sum_{i=1}^{n} \lambda_i} \] 设定阈值，比如要保留\(90\%\)的能量，则使上述比例大于\(0.9\)，最小的\(r\)值作为主成分的数量。

实例：对半导体制造数据降维

为了提高计算效率，往往需要对数据进行降维处理。MLiA一书中使用一个半导体制造数据，该数据集共有590个特征，通过对比特征值的大小发现，只有部分特征是重要的，其他的特征可以忽略，从而可以大大压缩数据规模，提高计算效率。

1
2
3
4
5
6
7
8
9
def replaceNanWithMean():
    dataMat = loadDataSet('secom.data', ' ')
    numFeat = shape(dataMat)[1]
    for i in range(numFeat) :
        # 计算非NaN值的平均值
        meanVal = mean(dataMat[nonzero(~isnan(dataMat[:,i].A))[0],i])
        # 将所有NaN替换为平均值
        dataMat[nonzero(isnan(dataMat[:,i].A))[0],i] = meanVal
    return dataMat
1
2
3
4
5
dataMat = replaceNanWithMean()
meanVals = mean(dataMat, axis=0)
meanRemoved = dataMat - meanVals
covMat = cov(meanRemoved, rowvar=0)
eigVals, eigVects = linalg.eig(mat(covMat))
1
2
3
4
5
6
7
8
9
10
11
12
eigValInd = argsort(eigVals)            #sort, sort goes smallest to largest
eigValInd = eigValInd[::-1]#reverse
sortedEigVals = eigVals[eigValInd]
total = sum(sortedEigVals)
varPercentage = sortedEigVals/total*100

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(1, 21), varPercentage[:20], marker='^')
plt.xlabel('Principal Component Number')
plt.ylabel('Percentage of Variance')
plt.show()
png

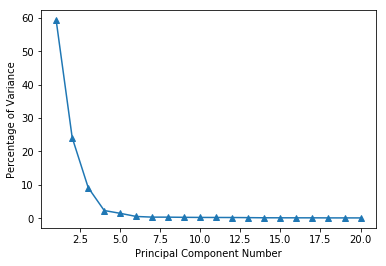
png

结论及讨论

结论

PCA方法有两个好处：一是数据压缩，提高算法效率；二是有利于数据可视化，找出重要特征。

讨论

  1. PCA方法只消除了特征之间的线性相关性，对于非线性相关性，可以考虑采用核函数的方法；
  2. PCA方法是一种无参技术，但是无法人为介入控制；
  3. 除了PCA之外，还有一些其他的降维技术，包括ICA(Independent Component Analysis)、LDA(Linear Discriminant Analysis)等。

参考资料

  1. Peter Harrington, Machine learning in action, Manning Publications, 2012
  2. 周志华，机器学习，清华大学出版社， 2016