单个隐藏层的神经网络

发表于 | 分类于

逻辑回归可以看做只有输入和输出层的神经网络，本文介绍单个隐藏层的神经网络，并应用其进行二分类，利用非线性激活函数对线性不可分数据进行预测。涉及包括非线性激活函数的种类和功能、隐藏层的作用、梯度的计算等内容。

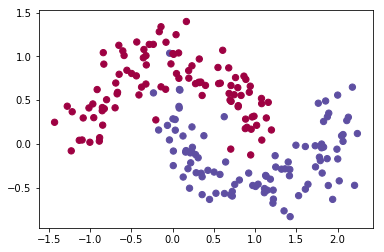
数据加载

1
2
3
4
5
6
7
8
9
10
11
12
# Package imports
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets

%matplotlib inline

np.random.seed(1) # set a seed so that the results are consistent
1
X, Y = load_planar_dataset()
1
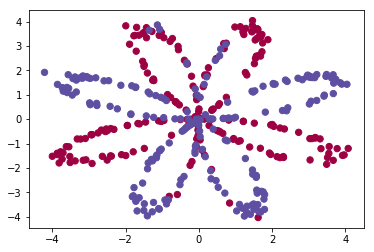
2
# Visualize the data:
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);
png

png

数据包括:
- 矩阵X，每个样本包含两个特征(x1, x2)
- 向量Y，每个样本取值0/1(红色:0, 蓝色:1).

1
2
3
4
5
6
7
8
9
### START CODE HERE ### (≈ 3 lines of code)
shape_X = X.shape
shape_Y = Y.shape
m =  Y.size # training set size
### END CODE HERE ###

print ('The shape of X is: ' + str(shape_X))
print ('The shape of Y is: ' + str(shape_Y))
print ('I have m = %d training examples!' % (m))
The shape of X is: (2, 400)
The shape of Y is: (1, 400)
I have m = 400 training examples!

逻辑回归

为了对比逻辑回归的效果，采用sklearn自带的逻辑回归算法进行测试

1
2
3
# Train the logistic regression classifier
clf = sklearn.linear_model.LogisticRegressionCV();
clf.fit(X.T, Y.T);
/home/seisinv/anaconda3/envs/tensorflow/lib/python3.5/site-packages/sklearn/utils/validation.py:547: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  y = column_or_1d(y, warn=True)
1
2
3
4
5
6
7
8
# Plot the decision boundary for logistic regression
plot_decision_boundary(lambda x: clf.predict(x), X, Y)
plt.title("Logistic Regression")

# Print accuracy
LR_predictions = clf.predict(X.T)
print ('Accuracy of logistic regression: %d ' % float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) +
       '% ' + "(percentage of correctly labelled datapoints)")
Accuracy of logistic regression: 47 % (percentage of correctly labelled datapoints)
png

png

小结：由于数据不是线性可分的，所以逻辑回归表现不好。

神经网络模型

模型图: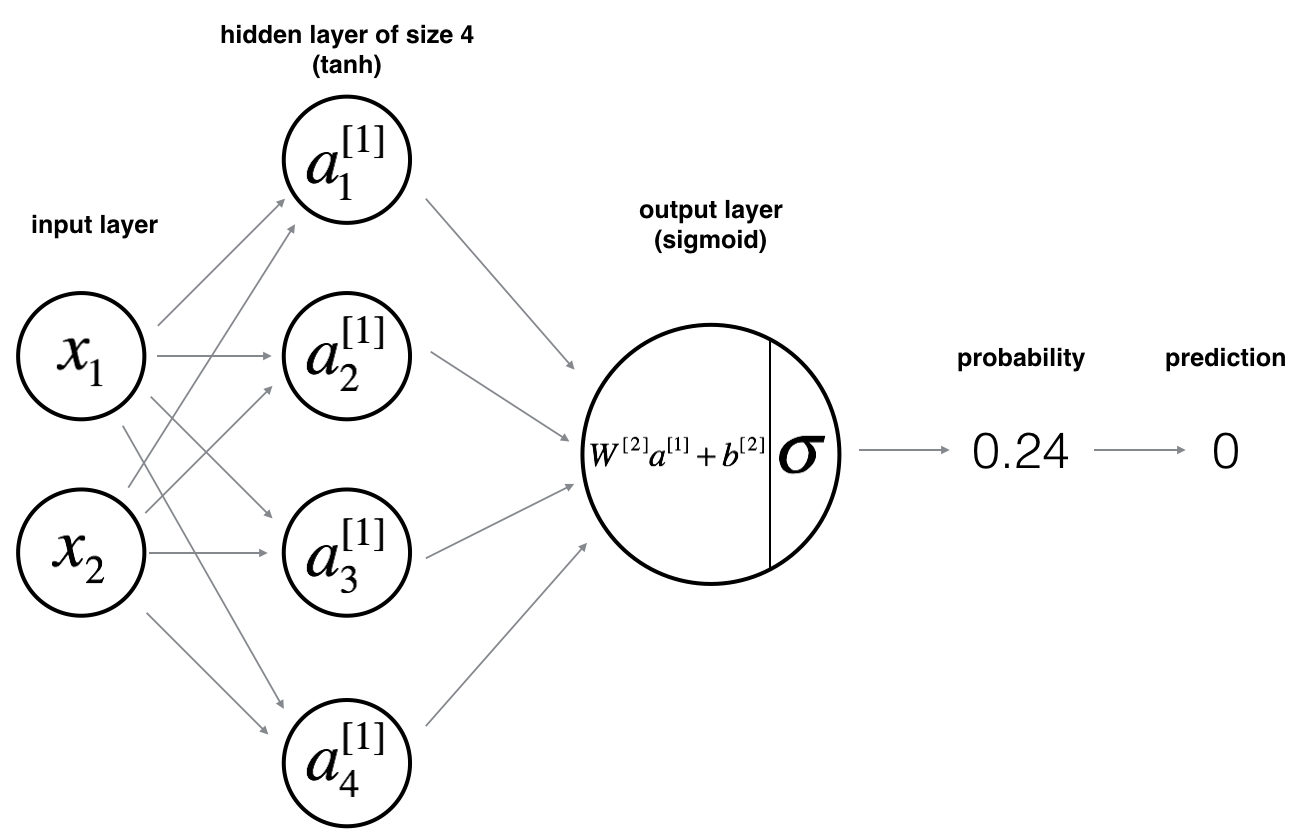

数学公式:

对一个样本 \(x^{(i)}\): \[z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1] (i)}\tag{1}\] \[a^{[1] (i)} = \tanh(z^{[1] (i)})\tag{2}\] \[z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2] (i)}\tag{3}\] \[\hat{y}^{(i)} = a^{[2] (i)} = \sigma(z^{ [2] (i)})\tag{4}\] \[y^{(i)}_{prediction} = \begin{cases} 1 & \mbox{if } a^{[2](i)} > 0.5 \\ 0 & \mbox{otherwise } \end{cases}\tag{5}\]

给定所有样本的预测值，计算代价函数 \(J\) : \[J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large\left(\small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large \right) \small \tag{6}\]

流程: 1. 定义神经网络结构 ( 输入单元个数、隐藏层神经元个数等). 2. 模型参数初始化 3. 循环: - 正向传播 - 计算损失函数 - 反传计算梯度 - 更新参数（梯度下降法）

定义神经网络结构

对于单隐藏层神经网络，关于神经网络结构有三个超参: - n_x: 输入层大小 - n_h: 隐藏层大小 （本文定义为4） - n_y: 输出层大小

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# GRADED FUNCTION: layer_sizes

def layer_sizes(X, Y):
    """
    Arguments:
    X -- input dataset of shape (input size, number of examples)
    Y -- labels of shape (output size, number of examples)
    
    Returns:
    n_x -- the size of the input layer
    n_h -- the size of the hidden layer
    n_y -- the size of the output layer
    """
    ### START CODE HERE ### (≈ 3 lines of code)
    n_x = X.shape[0] # size of input layer
    n_h = 4
    n_y = Y.shape[0] # size of output layer
    ### END CODE HERE ###
    return (n_x, n_h, n_y)
1
2
3
4
5
X_assess, Y_assess = layer_sizes_test_case()
(n_x, n_h, n_y) = layer_sizes(X_assess, Y_assess)
print("The size of the input layer is: n_x = " + str(n_x))
print("The size of the hidden layer is: n_h = " + str(n_h))
print("The size of the output layer is: n_y = " + str(n_y))
The size of the input layer is: n_x = 5
The size of the hidden layer is: n_h = 4
The size of the output layer is: n_y = 2

初始化模型参数

利用随机函数初始化模型参数w，零初始化b。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# GRADED FUNCTION: initialize_parameters

def initialize_parameters(n_x, n_h, n_y):
    """
    Argument:
    n_x -- size of the input layer
    n_h -- size of the hidden layer
    n_y -- size of the output layer
    
    Returns:
    params -- python dictionary containing your parameters:
                    W1 -- weight matrix of shape (n_h, n_x)
                    b1 -- bias vector of shape (n_h, 1)
                    W2 -- weight matrix of shape (n_y, n_h)
                    b2 -- bias vector of shape (n_y, 1)
    """
    
    np.random.seed(2) # we set up a seed so that your output matches ours although the initialization is random.
    
    ### START CODE HERE ### (≈ 4 lines of code)
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))
    ### END CODE HERE ###
    
    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters
1
2
3
4
5
6
7
n_x, n_h, n_y = initialize_parameters_test_case()

parameters = initialize_parameters(n_x, n_h, n_y)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[-0.00416758 -0.00056267]
 [-0.02136196  0.01640271]
 [-0.01793436 -0.00841747]
 [ 0.00502881 -0.01245288]]
b1 = [[ 0.]
 [ 0.]
 [ 0.]
 [ 0.]]
W2 = [[-0.01057952 -0.00909008  0.00551454  0.02292208]]
b2 = [[ 0.]]

循环迭代

  • 激活函数既可以采用sigmoid函数（已经实现）和tanh函数（np.tanh());
  • 具体步骤包括:
    1. 从字典"parameters"中读取参数
    2. 正传，计算 \(Z^{[1]}, A^{[1]}, Z^{[2]}\) and \(A^{[2]}\)
  • 反传中需要的变量都存在"cache"中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# GRADED FUNCTION: forward_propagation

def forward_propagation(X, parameters):
    """
    Argument:
    X -- input data of size (n_x, m)
    parameters -- python dictionary containing your parameters (output of initialization function)
    
    Returns:
    A2 -- The sigmoid output of the second activation
    cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
    """
    # Retrieve each parameter from the dictionary "parameters"
    ### START CODE HERE ### (≈ 4 lines of code)
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    #print(W1.shape, b1.shape, W2.shape, b2.shape)
    
    ### END CODE HERE ###
    
    # Implement Forward Propagation to calculate A2 (probabilities)
    ### START CODE HERE ### (≈ 4 lines of code)
    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = sigmoid(Z2)
    ### END CODE HERE ###
    
    assert(A2.shape == (1, X.shape[1]))
    
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    
    return A2, cache
1
2
3
4
5
6
X_assess, parameters = forward_propagation_test_case()

A2, cache = forward_propagation(X_assess, parameters)

# Note: we use the mean here just to make sure that your output matches ours. 
print(np.mean(cache['Z1']) ,np.mean(cache['A1']),np.mean(cache['Z2']),np.mean(cache['A2']))
-0.000499755777742 -0.000496963353232 0.000438187450959 0.500109546852

计算好了\(A^{[2]}\) (Python 变量为 "A2"), 它包含了每个样本\(a^{[2](i)}\) , 那么可以根据下面的公式计算代价函数: \[J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large{(} \small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large{)} \small\tag{13}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# GRADED FUNCTION: compute_cost

def compute_cost(A2, Y, parameters):
    """
    Computes the cross-entropy cost given in equation (13)
    
    Arguments:
    A2 -- The sigmoid output of the second activation, of shape (1, number of examples)
    Y -- "true" labels vector of shape (1, number of examples)
    parameters -- python dictionary containing your parameters W1, b1, W2 and b2
    
    Returns:
    cost -- cross-entropy cost given equation (13)
    """
    
    m = Y.shape[1] # number of example
    
    # Retrieve W1 and W2 from parameters
    ### START CODE HERE ### (≈ 2 lines of code)
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    ### END CODE HERE ###
    
    # Compute the cross-entropy cost
    ### START CODE HERE ### (≈ 2 lines of code)
    logprobs = np.multiply(np.log(A2), Y) + np.multiply((1-Y), np.log(1-A2))
    ### END CODE HERE ###
    cost = -1/m * np.sum(logprobs) 
    
    cost = np.squeeze(cost)     # makes sure cost is the dimension we expect. 
                                # E.g., turns [[17]] into 17 
    assert(isinstance(cost, float))
    
    return cost
1
2
3
A2, Y_assess, parameters = compute_cost_test_case()

print("cost = " + str(compute_cost(A2, Y_assess, parameters)))
cost = 0.692919893776

反传是神经网络中（数学上）最复杂的一步：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# GRADED FUNCTION: backward_propagation

def backward_propagation(parameters, cache, X, Y):
    """
    Implement the backward propagation using the instructions above.
    
    Arguments:
    parameters -- python dictionary containing our parameters 
    cache -- a dictionary containing "Z1", "A1", "Z2" and "A2".
    X -- input data of shape (2, number of examples)
    Y -- "true" labels vector of shape (1, number of examples)
    
    Returns:
    grads -- python dictionary containing your gradients with respect to different parameters
    """
    m = X.shape[1]
    
    # First, retrieve W1 and W2 from the dictionary "parameters".
    ### START CODE HERE ### (≈ 2 lines of code)
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    ### END CODE HERE ###
        
    # Retrieve also A1 and A2 from dictionary "cache".
    ### START CODE HERE ### (≈ 2 lines of code)
    A1 = cache["A1"]
    A2 = cache["A2"]
    ### END CODE HERE ###
    
    # Backward propagation: calculate dW1, db1, dW2, db2. 
    ### START CODE HERE ### (≈ 6 lines of code, corresponding to 6 equations on slide above)
    dZ2= A2 - Y
    dW2 = (1/m) * np.dot(dZ2, A1.T)
    db2 = (1/m) * np.sum(dZ2, axis=1, keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T, dZ2), (1 - np.power(A1, 2)))
    dW1 = (1/m) * np.dot(dZ1, X.T)
    db1 = (1/m) * np.sum(dZ1, axis=1, keepdims=True)
    ### END CODE HERE ###
    
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    
    return grads
1
2
3
4
5
6
7
parameters, cache, X_assess, Y_assess = backward_propagation_test_case()

grads = backward_propagation(parameters, cache, X_assess, Y_assess)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"]))
dW1 = [[ 0.01018708 -0.00708701]
 [ 0.00873447 -0.0060768 ]
 [-0.00530847  0.00369379]
 [-0.02206365  0.01535126]]
db1 = [[-0.00069728]
 [-0.00060606]
 [ 0.000364  ]
 [ 0.00151207]]
dW2 = [[ 0.00363613  0.03153604  0.01162914 -0.01318316]]
db2 = [[ 0.06589489]]

梯度下降法准则：$ = - $，其中 \(\alpha\) 是学习率， \(\theta\) 代表待求的参数.

当学习率合理时，梯度下降法收敛；当学习率太小，收敛太慢；当学习率太大，容易发散。下面的图来自Adam Harley。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
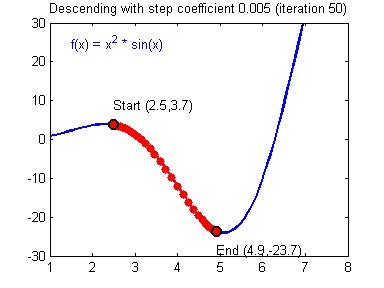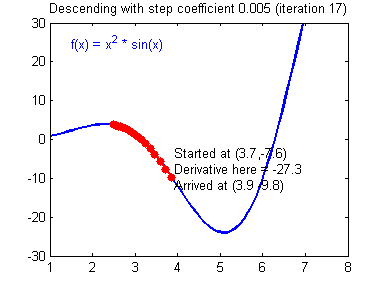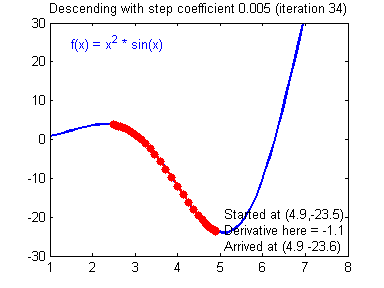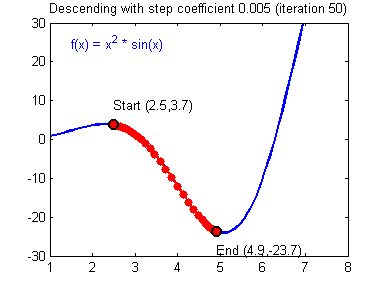
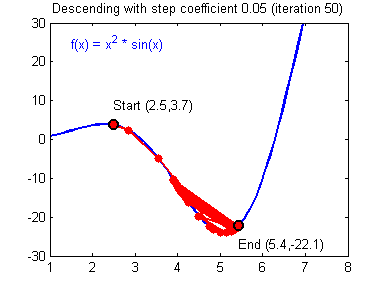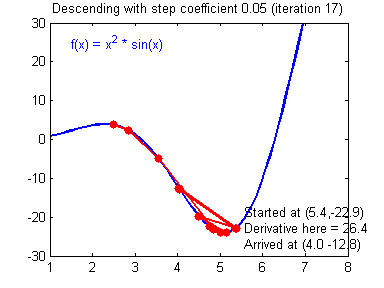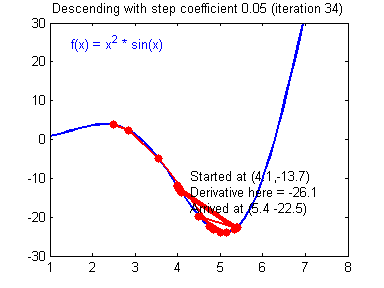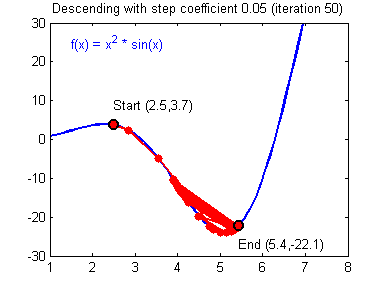
43
# GRADED FUNCTION: update_parameters

def update_parameters(parameters, grads, learning_rate = 1.2):
    """
    Updates parameters using the gradient descent update rule given above
    
    Arguments:
    parameters -- python dictionary containing your parameters 
    grads -- python dictionary containing your gradients 
    
    Returns:
    parameters -- python dictionary containing your updated parameters 
    """
    # Retrieve each parameter from the dictionary "parameters"
    ### START CODE HERE ### (≈ 4 lines of code)
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    ### END CODE HERE ###
    
    # Retrieve each gradient from the dictionary "grads"
    ### START CODE HERE ### (≈ 4 lines of code)
    dW1 = grads["dW1"]
    db1 = grads["db1"]
    dW2 = grads["dW2"]
    db2 = grads["db2"]
    ## END CODE HERE ###
    
    # Update rule for each parameter
    ### START CODE HERE ### (≈ 4 lines of code)
    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2
    ### END CODE HERE ###
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters
1
2
3
4
5
6
7
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)

print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[-0.00643025  0.01936718]
 [-0.02410458  0.03978052]
 [-0.01653973 -0.02096177]
 [ 0.01046864 -0.05990141]]
b1 = [[ -1.02420756e-06]
 [  1.27373948e-05]
 [  8.32996807e-07]
 [ -3.20136836e-06]]
W2 = [[-0.01041081 -0.04463285  0.01758031  0.04747113]]
b2 = [[ 0.00010457]]

整合成神经网络模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# GRADED FUNCTION: nn_model

def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
    """
    Arguments:
    X -- dataset of shape (2, number of examples)
    Y -- labels of shape (1, number of examples)
    n_h -- size of the hidden layer
    num_iterations -- Number of iterations in gradient descent loop
    print_cost -- if True, print the cost every 1000 iterations
    
    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
    """
    
    np.random.seed(3)
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[2]
    
    # Initialize parameters, then retrieve W1, b1, W2, b2. Inputs: "n_x, n_h, n_y". Outputs = "W1, b1, W2, b2, parameters".
    ### START CODE HERE ### (≈ 5 lines of code)
    parameters = initialize_parameters(n_x, n_h, n_y)
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    ### END CODE HERE ###
    
    # Loop (gradient descent)

    for i in range(0, num_iterations):
         
        ### START CODE HERE ### (≈ 4 lines of code)
        # Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
        A2, cache = forward_propagation(X, parameters)
        
        # Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
        cost = compute_cost(A2, Y, parameters)
 
        # Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
        grads = backward_propagation(parameters, cache, X, Y)
 
        # Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
        parameters = update_parameters(parameters, grads)
        
        ### END CODE HERE ###
        
        # Print the cost every 1000 iterations
        if print_cost and i % 1000 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))

    return parameters
1
2
3
4
5
6
7
X_assess, Y_assess = nn_model_test_case()

parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
/home/seisinv/anaconda3/envs/tensorflow/lib/python3.5/site-packages/ipykernel_launcher.py:26: RuntimeWarning: divide by zero encountered in log
/media/seisinv/Data/svn/ai/learn/dl_ng/planar_utils.py:34: RuntimeWarning: overflow encountered in exp
  s = 1/(1+np.exp(-x))


W1 = [[-4.18494056  5.33220609]
 [-7.52989382  1.24306181]
 [-4.1929459   5.32632331]
 [ 7.52983719 -1.24309422]]
b1 = [[ 2.32926819]
 [ 3.79458998]
 [ 2.33002577]
 [-3.79468846]]
W2 = [[-6033.83672146 -6008.12980822 -6033.10095287  6008.06637269]]
b2 = [[-52.66607724]]

预测

利用正传函数predict()预测

predictions = \(y_{prediction} = \mathbb 1 \textfalse = \begin{cases} 1 & \text{if}\ activation > 0.5 \\ 0 & \text{otherwise} \end{cases}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# GRADED FUNCTION: predict

def predict(parameters, X):
    """
    Using the learned parameters, predicts a class for each example in X
    
    Arguments:
    parameters -- python dictionary containing your parameters 
    X -- input data of size (n_x, m)
    
    Returns
    predictions -- vector of predictions of our model (red: 0 / blue: 1)
    """
    
    # Computes probabilities using forward propagation, and classifies to 0/1 using 0.5 as the threshold.
    ### START CODE HERE ### (≈ 2 lines of code)
    A2, cache = forward_propagation(X, parameters)
    predictions = (A2 > 0.5)  # Vectorized
    ### END CODE HERE ###
    
    return predictions
1
2
3
4
parameters, X_assess = predict_test_case()

predictions = predict(parameters, X_assess)
print("predictions mean = " + str(np.mean(predictions)))
predictions mean = 0.666666666667
1
2
3
4
5
6
# Build a model with a n_h-dimensional hidden layer
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)

# Plot the decision boundary
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
Cost after iteration 0: 0.693048
Cost after iteration 1000: 0.288083
Cost after iteration 2000: 0.254385
Cost after iteration 3000: 0.233864
Cost after iteration 4000: 0.226792
Cost after iteration 5000: 0.222644
Cost after iteration 6000: 0.219731
Cost after iteration 7000: 0.217504
Cost after iteration 8000: 0.219481
Cost after iteration 9000: 0.218565





<matplotlib.text.Text at 0x7f066c4ba940>
png

png

1
2
3
# Print accuracy
predictions = predict(parameters, X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')
Accuracy: 90%

调参：隐藏层神经元个数

1
2
3
4
5
6
7
8
9
10
11
12
# This may take about 2 minutes to run

plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(5, 2, i+1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters = nn_model(X, Y, n_h, num_iterations = 5000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
    print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))
Accuracy for 1 hidden units: 67.5 %
Accuracy for 2 hidden units: 67.25 %
Accuracy for 3 hidden units: 90.75 %
Accuracy for 4 hidden units: 90.5 %
Accuracy for 5 hidden units: 91.25 %
Accuracy for 20 hidden units: 90.0 %
Accuracy for 50 hidden units: 90.75 %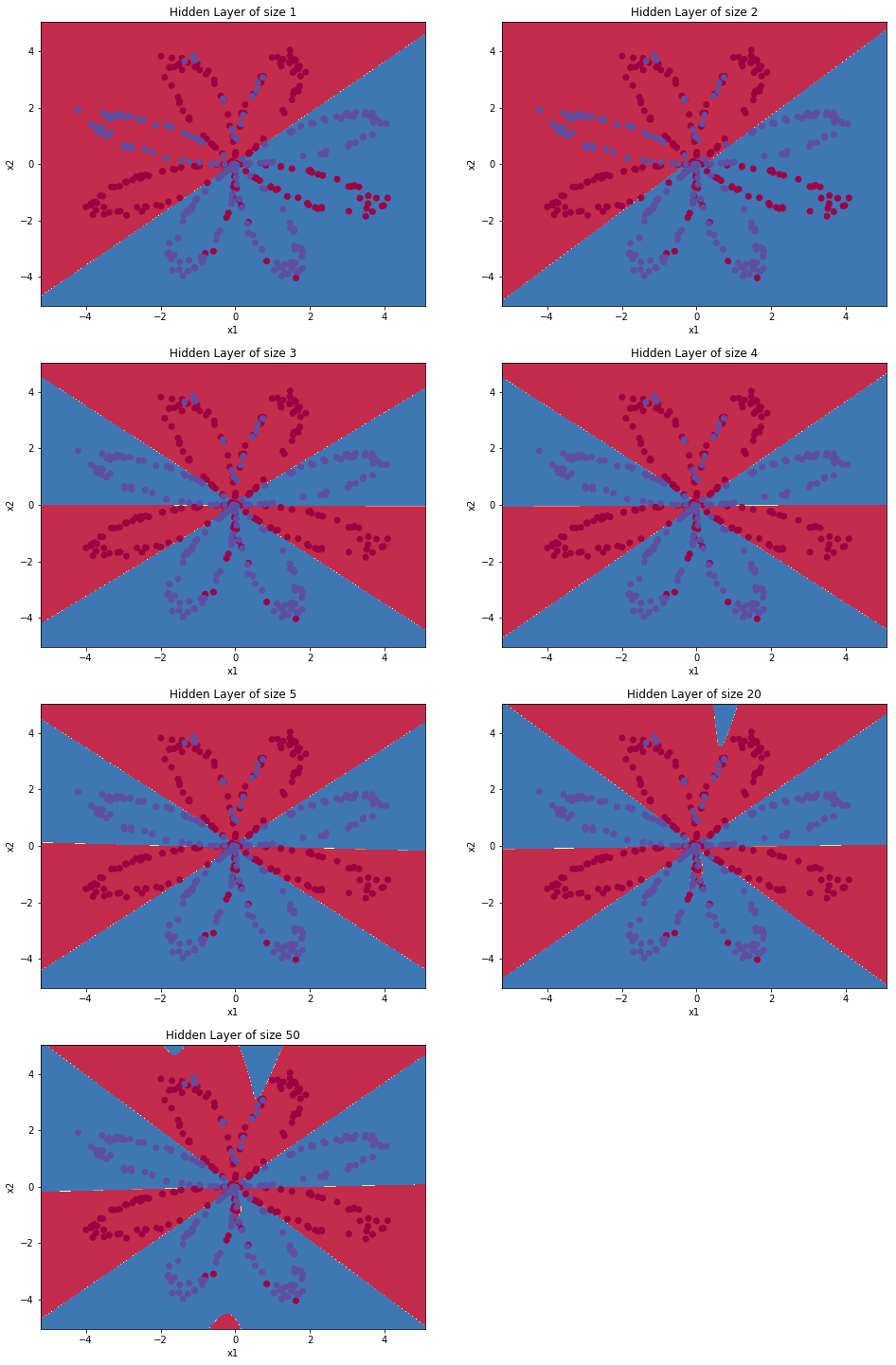
png

png

测试其他数据集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Datasets
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()

datasets = {"noisy_circles": noisy_circles,
            "noisy_moons": noisy_moons,
            "blobs": blobs,
            "gaussian_quantiles": gaussian_quantiles}

### START CODE HERE ### (choose your dataset)
dataset = "noisy_moons"
### END CODE HERE ###

X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])

# make blobs binary
if dataset == "blobs":
    Y = Y%2

# Visualize the data
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);
png

png

结论

  • 隐藏层神经元个数越多，越容易拟合训练数据，知道过拟合
  • 最佳的隐藏层神经元个数大概为5，既可以很好的拟合数据，也不会引入过拟合
  • 另一种既可以使用大的神经网络，又可以避免过拟合的方法是正则化。

附录

非线性激活函数的种类

  1. sigmoid函数
    \[ g(z) = \frac{1}{1+e^{-z}} \] 导数为： \[ g'(z) = g(z)(1-g(z)) \]

  2. tanh函数
    \[ g(z) = tanh(z) = \frac{e^z-e^{-z}}{e^z+e^{-z}} = 2*sigmoid(z) - 1 \] 导数为： \[ g'(z) = 1-g^2(z) \]

  3. ReLU函数 \[ g(z) = max(0,z) \] 导数为： \[ g'(z) = \begin{cases} 0 & \text{if}\ z < 0 \\ 1 & \text{if}\ z > 0 \\ \text{not defined} & \text{otherwise} \\ \end{cases} \]

  4. Leaky ReLU(Rectified Linear Unit)函数 \[ g(z) = max(\alpha z,z)\ 0\le z \le 1 \] 导数为： \[ g'(z) = \begin{cases} \alpha & \text{if}\ z < 0 \\ 1 & \text{if}\ z > 0 \\ \text{not defined} & \text{otherwise} \\ \end{cases} \]

  1. 大部分情况下，tanh函数（输出均值为0）都优于sigmoid函数，除非在输出层进行二分类时，必须使用sigmoid函数
  2. 当z很大或者很小时，sigmoid和tanh函数的梯度都很小，导致收敛速度很慢，因此默认情况下都是使用ReLU函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
z = np.arange(-20,20,0.1)

#sigmoid
g1 = 1/(1+np.exp(-z))
g1_der = g1*(1-g1)
plt.figure(1,figsize=(10, 4))
plt.subplot(121)
plt.title("Sigmoid")
plt.grid(True)
plt.plot(g1)
plt.subplot(122)
plt.title("Sigmoid derivative")
plt.grid(True)
plt.plot(g1_der)

# tanh
g1 = np.tanh(z)
g1_der = 1.0-g1*g1
plt.figure(2,figsize=(10, 4))
plt.subplot(121)
plt.title("Tanh")
plt.grid(True)
plt.plot(g1)
plt.subplot(122)
plt.title("Tanh derivative")
plt.grid(True)
plt.plot(g1_der)

# ReLU
g1 = np.maximum(0,z)
g1_der[z<=0]= 0
g1_der[z>0] = 1
plt.figure(3,figsize=(10, 4))
plt.subplot(121)
plt.title("ReLU")
plt.grid(True)
plt.plot(g1)
plt.subplot(122)
plt.title("ReLU derivative")
plt.grid(True)
plt.plot(g1_der)

# Leaky ReLU
a=0.1
g1 = np.maximum(a*z,z)
g1_der[z<=0]= a
g1_der[z>0] = 1
plt.figure(4,figsize=(10, 4))
plt.subplot(121)
plt.title("Leaky ReLU")
plt.grid(True)
plt.plot(g1)
plt.subplot(122)
plt.title("Leaky ReLU derivative")
plt.grid(True)
plt.plot(g1_der)
[<matplotlib.lines.Line2D at 0x7f065e7bdf60>]
png

png

png

png

png

png

png

png

为何要在隐藏层使用非线性激活函数

正传过程中，对一个样本 \(x^{(i)}\): \[z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1] (i)}\tag{1}\] \[a^{[1] (i)} = g^{[1]}(z^{[1] (i)})\tag{2}\] \[z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2] (i)}\tag{3}\] \[\hat{y}^{(i)} = a^{[2] (i)} = g^{[2]}(z^{ [2] (i)})\tag{4}\] 当\(g^{[1]}=g^{[2]}=I\)，可以证明： \[ a^{[2] (i)} = W'x^{(i)}+b' = (W^{[1]}W^{[2]})x^{(i)}+(W^{[2]}b^{[1] (i)}+b^{[2] (i)}) \] 也是说，当采用线性激活函数，神经网络等效于线性回归。 当输出为sigmoid函数，但是隐藏层使用线性激活函数，则深度神经网络依然和逻辑回归等效。

为何不能将深度神经网络的模型参数初始化为0

在逻辑回归算法中，模型参数初始化为0，但是在多于一层的神经网络中，不能将模型参数初始化为0。原因是：当W初始化为0，各个神经元计算的结果相同，W的更新量每一行也相同，也就没有必要增加神经元的个数了，这是著名的Symmetric breaking问题。解决办法是初始化W为随机向量，例如\(W^{[1]}=np.random.randn(n^{[1]},n^{[0]})*0.01;b^{[1]}=np.zeros((n^{[1]},1))\)，其中取比较小的\(0.01\)是为了使得作为sigmoid函数的输入不要太大，不然容易导致梯度饱和（梯度接近于0），降低收敛速度。

参考资料