深度神经网络在图像分类中的应用

发表于 | 分类于

本文介绍深度神经网络的一个主要应用：计算机视觉。对比逻辑回归，浅层神经网络在图像分类中的性能，说明深度神经网络在图像分类中的应用价值。

预处理

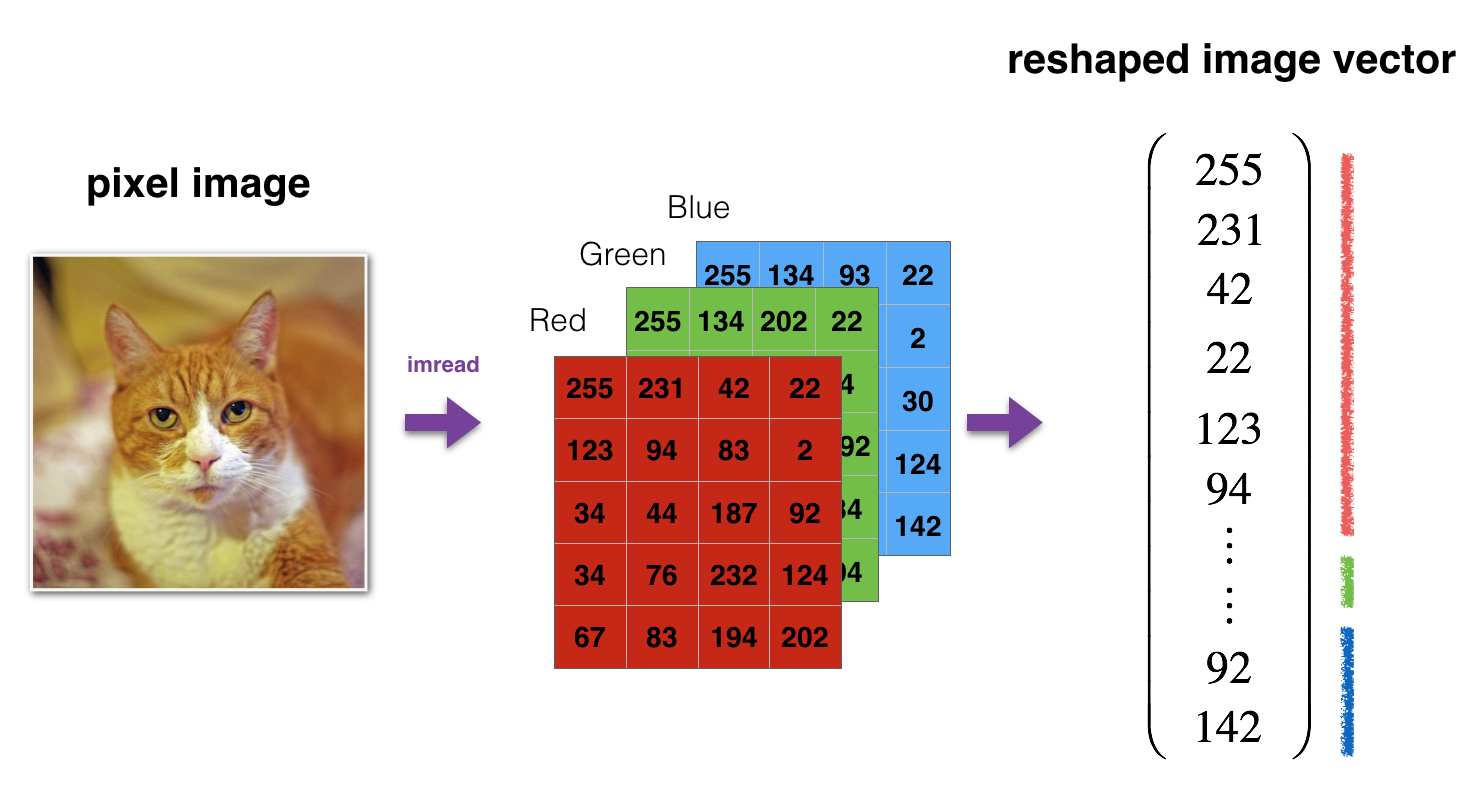
预处理包括：将图像向量化以及对像素的标准化

Figure 1: Image to vector conversion. 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import time
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
from dnn_app_utils_v2 import *

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

np.random.seed(1)
1
train_x_orig, train_y, test_x_orig, test_y, classes = load_data()
1
2
3
4
# Example of a picture
index = 100
plt.imshow(train_x_orig[index])
print ("y = " + str(train_y[0,index]) + ". It's a " + classes[train_y[0,index]].decode("utf-8") +  " picture.")
y = 0. It's a non-cat picture.
png

png

1
2
3
4
5
6
7
8
9
10
11
12
# Explore your dataset 
m_train = train_x_orig.shape[0]
num_px = train_x_orig.shape[1]
m_test = test_x_orig.shape[0]

print ("Number of training examples: " + str(m_train))
print ("Number of testing examples: " + str(m_test))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_x_orig shape: " + str(train_x_orig.shape))
print ("train_y shape: " + str(train_y.shape))
print ("test_x_orig shape: " + str(test_x_orig.shape))
print ("test_y shape: " + str(test_y.shape))
Number of training examples: 209
Number of testing examples: 50
Each image is of size: (64, 64, 3)
train_x_orig shape: (209, 64, 64, 3)
train_y shape: (1, 209)
test_x_orig shape: (50, 64, 64, 3)
test_y shape: (1, 50)
1
2
3
4
5
6
7
8
9
10
# Reshape the training and test examples 
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T   # The "-1" makes reshape flatten the remaining dimensions
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0], -1).T

# Standardize data to have feature values between 0 and 1.
train_x = train_x_flatten/255.
test_x = test_x_flatten/255.

print ("train_x's shape: " + str(train_x.shape))
print ("test_x's shape: " + str(test_x.shape))
train_x's shape: (12288, 209)
test_x's shape: (12288, 50)

神经网络的架构

本文对比两种架构，一种是2层神经网络，一种是更深的神经网络。

两层神经网络

Figure 2: 两层神经网络.
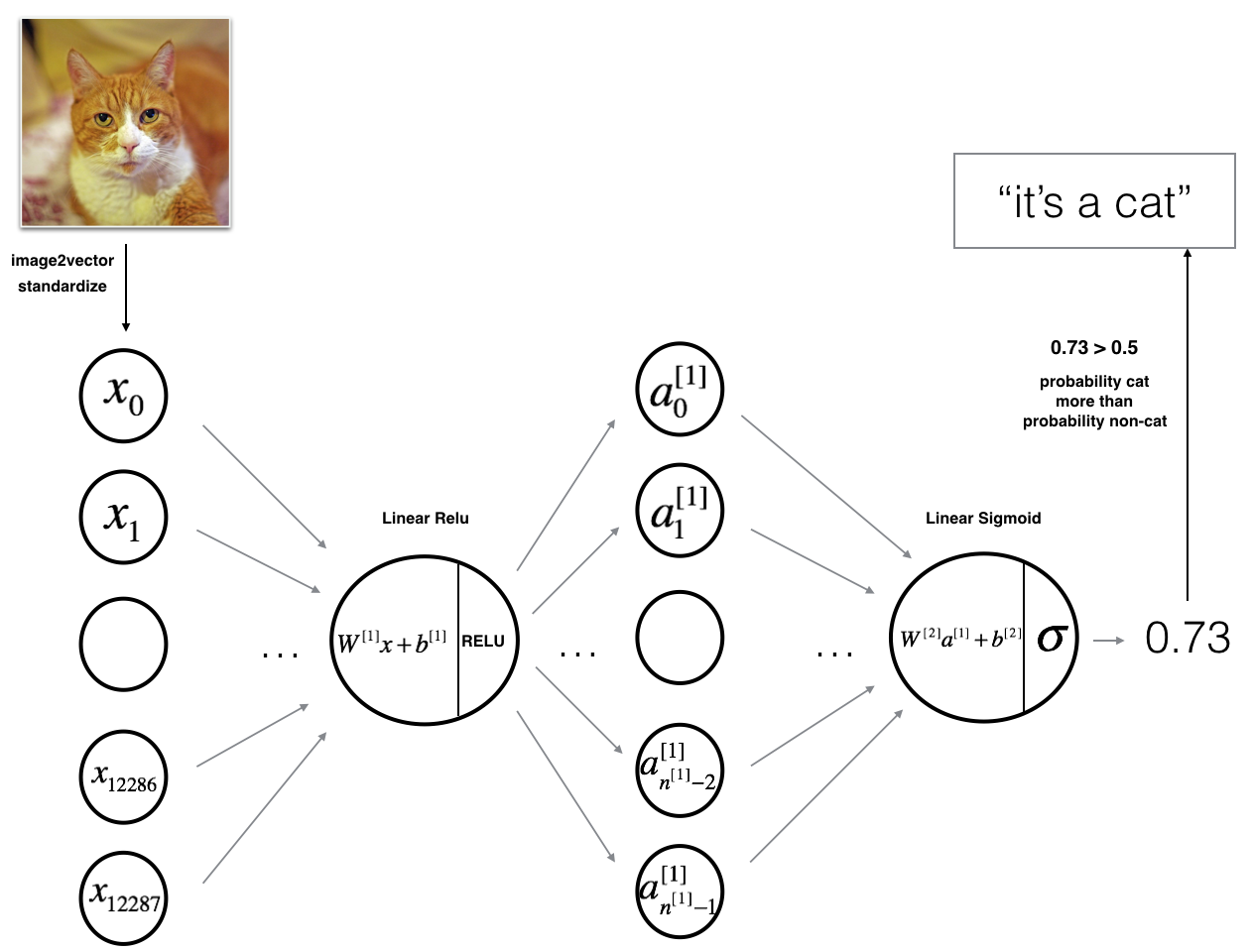
模型可以总结为: INPUT -> LINEAR -> RELU -> LINEAR -> SIGMOID -> OUTPUT.

图2的细节: - 输入图像 (64,64,3) 整形为大小为 \((12288,1)\) 的向量. - 对应的向量: \([x_0,x_1,...,x_{12287}]^T\) 乘以大小为\((n^{[1]}, 12288)\)的加权矩阵 \(W^{[1]}\). - 加上偏移量，并取RELU: \([a_0^{[1]}, a_1^{[1]},..., a_{n^{[1]}-1}^{[1]}]^T\). - 重复上述过程. - 乘以\(W^{[2]}\) 并加上截距 (偏移量). - 最终取结果的sigmoid响应. 如果大于 0.5, 分类为猫.

\(L\)层深度神经网络

Figure 3: L层神经网络.
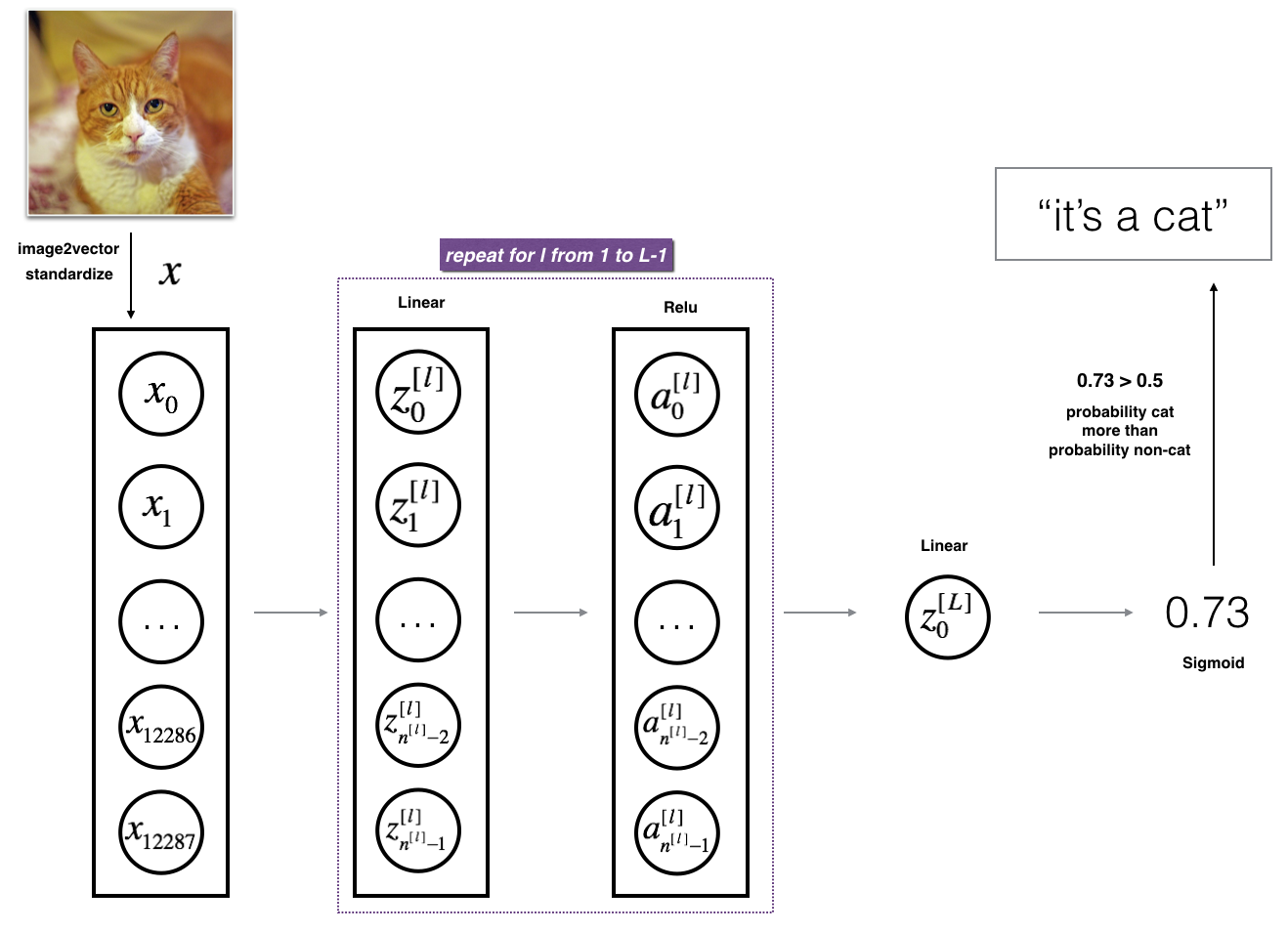
模型可以总结为: [LINEAR -> RELU] \(\times\) (L-1) -> LINEAR -> SIGMOID

图3的细节: - 输入图像 (64,64,3) 整形为大小为 \((12288,1)\) 的向量. - 对应的向量: \([x_0,x_1,...,x_{12287}]^T\) 乘以大小为\((n^{[1]}, 12288)\)的加权矩阵 \(W^{[1]}\). - 加上偏移量，并取RELU: \([a_0^{[1]}, a_1^{[1]},..., a_{n^{[1]}-1}^{[1]}]^T\). - 根据模型的架构，对每对 \((W^{[l]}, b^{[l]})\) 重复多次. - 最终, 取最后一层线性单元的sigmoid响应. 如果大于 0.5, 分类为猫.

实现方法

方法如下: 1. 初始化参数、定义超参 2. 循环num_iterations次: a. 正传 b. 计算代价函数 c. 反传 d. 更新模型 4. 利用训练的参数进行预测

两层网络

1
2
3
4
5
### CONSTANTS DEFINING THE MODEL ####
n_x = 12288     # num_px * num_px * 3
n_h = 7
n_y = 1
layers_dims = (n_x, n_h, n_y)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
# GRADED FUNCTION: two_layer_model

def two_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
    """
    Implements a two-layer neural network: LINEAR->RELU->LINEAR->SIGMOID.
    
    Arguments:
    X -- input data, of shape (n_x, number of examples)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
    layers_dims -- dimensions of the layers (n_x, n_h, n_y)
    num_iterations -- number of iterations of the optimization loop
    learning_rate -- learning rate of the gradient descent update rule
    print_cost -- If set to True, this will print the cost every 100 iterations 
    
    Returns:
    parameters -- a dictionary containing W1, W2, b1, and b2
    """
    
    np.random.seed(1)
    grads = {}
    costs = []                              # to keep track of the cost
    m = X.shape[1]                           # number of examples
    (n_x, n_h, n_y) = layers_dims
    
    # Initialize parameters dictionary, by calling one of the functions you'd previously implemented
    ### START CODE HERE ### (≈ 1 line of code)
    parameters = initialize_parameters(n_x, n_h, n_y)
    ### END CODE HERE ###
    
    # Get W1, b1, W2 and b2 from the dictionary parameters.
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # Loop (gradient descent)

    for i in range(0, num_iterations):

        # Forward propagation: LINEAR -> RELU -> LINEAR -> SIGMOID. Inputs: "X, W1, b1". Output: "A1, cache1, A2, cache2".
        ### START CODE HERE ### (≈ 2 lines of code)
        A1, cache1 = linear_activation_forward(X, W1, b1, activation='relu')
        A2, cache2 = linear_activation_forward(A1, W2, b2, activation='sigmoid')
        ### END CODE HERE ###
        
        # Compute cost
        ### START CODE HERE ### (≈ 1 line of code)
        cost = compute_cost(A2, Y)
        ### END CODE HERE ###
        
        # Initializing backward propagation
        dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
        
        # Backward propagation. Inputs: "dA2, cache2, cache1". Outputs: "dA1, dW2, db2; also dA0 (not used), dW1, db1".
        ### START CODE HERE ### (≈ 2 lines of code)
        dA1, dW2, db2 = linear_activation_backward(dA2, cache2, activation='sigmoid')
        dA0, dW1, db1 = linear_activation_backward(dA1, cache1, activation='relu')
        ### END CODE HERE ###
        
        # Set grads['dWl'] to dW1, grads['db1'] to db1, grads['dW2'] to dW2, grads['db2'] to db2
        grads['dW1'] = dW1
        grads['db1'] = db1
        grads['dW2'] = dW2
        grads['db2'] = db2
        
        # Update parameters.
        ### START CODE HERE ### (approx. 1 line of code)
        parameters = update_parameters(parameters, grads, learning_rate=learning_rate)
        ### END CODE HERE ###

        # Retrieve W1, b1, W2, b2 from parameters
        W1 = parameters["W1"]
        b1 = parameters["b1"]
        W2 = parameters["W2"]
        b2 = parameters["b2"]
        
        # Print the cost every 100 training example
        if print_cost and i % 100 == 0:
            print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
        if print_cost and i % 100 == 0:
            costs.append(cost)
       
    # plot the cost

    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per tens)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
    
    return parameters
1
parameters = two_layer_model(train_x, train_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True)
Cost after iteration 0: 0.6930497356599888
Cost after iteration 100: 0.6464320953428849
Cost after iteration 200: 0.6325140647912678
Cost after iteration 300: 0.6015024920354665
Cost after iteration 400: 0.5601966311605748
Cost after iteration 500: 0.5158304772764729
Cost after iteration 600: 0.4754901313943325
Cost after iteration 700: 0.43391631512257495
Cost after iteration 800: 0.4007977536203889
Cost after iteration 900: 0.3580705011323798
Cost after iteration 1000: 0.33942815383664127
Cost after iteration 1100: 0.3052753636196264
Cost after iteration 1200: 0.27491377282130164
Cost after iteration 1300: 0.24681768210614818
Cost after iteration 1400: 0.19850735037466105
Cost after iteration 1500: 0.17448318112556663
Cost after iteration 1600: 0.17080762978096006
Cost after iteration 1700: 0.11306524562164738
Cost after iteration 1800: 0.09629426845937156
Cost after iteration 1900: 0.08342617959726865
Cost after iteration 2000: 0.07439078704319083
Cost after iteration 2100: 0.06630748132267933
Cost after iteration 2200: 0.05919329501038172
Cost after iteration 2300: 0.05336140348560558
Cost after iteration 2400: 0.04855478562877019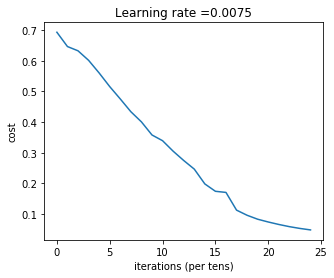
png

png

1
predictions_train = predict(train_x, train_y, parameters)
Accuracy: 1.0
1
predictions_test = predict(test_x, test_y, parameters)
Accuracy: 0.72

注意: 在1500步的结果也许可以得到更好的准确度，提前终止也是一种避免过拟合的方法。两层神经网络的表现优于逻辑回归（前面的结果70%）。

L层深层网络

1
2
### CONSTANTS ###
layers_dims = [12288, 20, 7, 5, 1] #  4-layer model
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
# GRADED FUNCTION: L_layer_model

def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):#lr was 0.009
    """
    Implements a L-layer neural network: [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID.
    
    Arguments:
    X -- data, numpy array of shape (number of examples, num_px * num_px * 3)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
    layers_dims -- list containing the input size and each layer size, of length (number of layers + 1).
    learning_rate -- learning rate of the gradient descent update rule
    num_iterations -- number of iterations of the optimization loop
    print_cost -- if True, it prints the cost every 100 steps
    
    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
    """

    np.random.seed(1)
    costs = []                         # keep track of cost
    
    # Parameters initialization.
    ### START CODE HERE ###
    parameters = initialize_parameters_deep(layers_dims)
    ### END CODE HERE ###
    
    # Loop (gradient descent)
    for i in range(0, num_iterations):

        # Forward propagation: [LINEAR -> RELU]*(L-1) -> LINEAR -> SIGMOID.
        ### START CODE HERE ### (≈ 1 line of code)
        AL, caches = L_model_forward(X, parameters)
        ### END CODE HERE ###
        
        # Compute cost.
        ### START CODE HERE ### (≈ 1 line of code)
        cost = compute_cost(AL, Y)
        ### END CODE HERE ###
    
        # Backward propagation.
        ### START CODE HERE ### (≈ 1 line of code)
        grads = L_model_backward(AL, Y, caches)
        ### END CODE HERE ###
 
        # Update parameters.
        ### START CODE HERE ### (≈ 1 line of code)
        parameters = update_parameters(parameters, grads, learning_rate=learning_rate)
        ### END CODE HERE ###
                
        # Print the cost every 100 training example
        if print_cost and i % 100 == 0:
            print ("Cost after iteration %i: %f" %(i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost)
            
    # plot the cost
    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per tens)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
    
    return parameters
1
parameters = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)
Cost after iteration 0: 0.771749
Cost after iteration 100: 0.672053
Cost after iteration 200: 0.648263
Cost after iteration 300: 0.611507
Cost after iteration 400: 0.567047
Cost after iteration 500: 0.540138
Cost after iteration 600: 0.527930
Cost after iteration 700: 0.465477
Cost after iteration 800: 0.369126
Cost after iteration 900: 0.391747
Cost after iteration 1000: 0.315187
Cost after iteration 1100: 0.272700
Cost after iteration 1200: 0.237419
Cost after iteration 1300: 0.199601
Cost after iteration 1400: 0.189263
Cost after iteration 1500: 0.161189
Cost after iteration 1600: 0.148214
Cost after iteration 1700: 0.137775
Cost after iteration 1800: 0.129740
Cost after iteration 1900: 0.121225
Cost after iteration 2000: 0.113821
Cost after iteration 2100: 0.107839
Cost after iteration 2200: 0.102855
Cost after iteration 2300: 0.100897
Cost after iteration 2400: 0.092878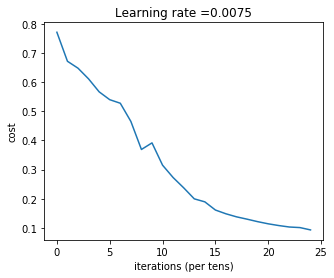
png

png

1
pred_train = predict(train_x, train_y, parameters)
Accuracy: 0.985645933014
1
pred_test = predict(test_x, test_y, parameters)
Accuracy: 0.8

注意: 可以看出，结果要优于两层网络。进一步的，可以通过调参（学习率、层数、神经元个数、迭代次数等）改善结果。

结果分析

1
print_mislabeled_images(classes, test_x, test_y, pred_test)
png

png

分析结果发现，错分的图像包括：

  • 猫的姿势特殊
  • 猫出现在和它类似的背景上
  • 猫的颜色和品种特殊
  • 摄像头角度问题
  • 图像的色度
  • 尺度问题

通过分析，可以进一步采集新数据或者合成数据，改善性能。

测试用户的图像

1
2
3
4
5
6
7
8
9
10
11
12
## START CODE HERE ##
my_image = "my_image.jpg" # change this to the name of your image file 
my_label_y = [1] # the true class of your image (1 -> cat, 0 -> non-cat)
## END CODE HERE ##

fname = "images/" + my_image
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(num_px,num_px)).reshape((num_px*num_px*3,1))
my_predicted_image = predict(my_image, my_label_y, parameters)

plt.imshow(image)
print ("y = " + str(np.squeeze(my_predicted_image)) + ", your L-layer model predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") +  "\" picture.")
Accuracy: 1.0
y = 1.0, your L-layer model predicts a "cat" picture.
png

png

参考资料