梯度验证

发表于 | 分类于

神经网络的反向传播过程中，梯度计算十分重要。如果梯度计算有误，模型训练很难保证收敛。本文介绍一种验证梯度计算是否正确的方法，该方法简单有效，但是计算比较耗时，往往不会在每次训练过程中都进行验证，而是在需要确保梯度正确的时候才使用。

方法原理

求导（或梯度）的定义: \[ \frac{\partial J}{\partial \theta} = \lim_{\varepsilon \to 0} \frac{J(\theta + \varepsilon) - J(\theta - \varepsilon)}{2 \varepsilon} \tag{1}\]

已知条件:

  • \(\frac{\partial J}{\partial \theta}\) 为待验证的目标.
  • \(J\) 计算完全正确，可以计算 \(J(\theta + \varepsilon)\) 和 \(J(\theta - \varepsilon)\) (其中 \(\theta\) 为实数).

因此可以利用公式 (1) 和一个小量 \(\varepsilon\) 来验证 \(\frac{\partial J}{\partial \theta}\) 是正确的!

一维梯度验证

考虑一维线性函数 \(J(\theta) = \theta x\). 模型只包含一个实数参数 \(\theta\), \(x\) 为输入.

下面计算 \(J(.)\) 和它的导数 \(\frac{\partial J}{\partial \theta}\). 再验证 \(J\)的导数是正确的.

图 1 : 1D 线性模型

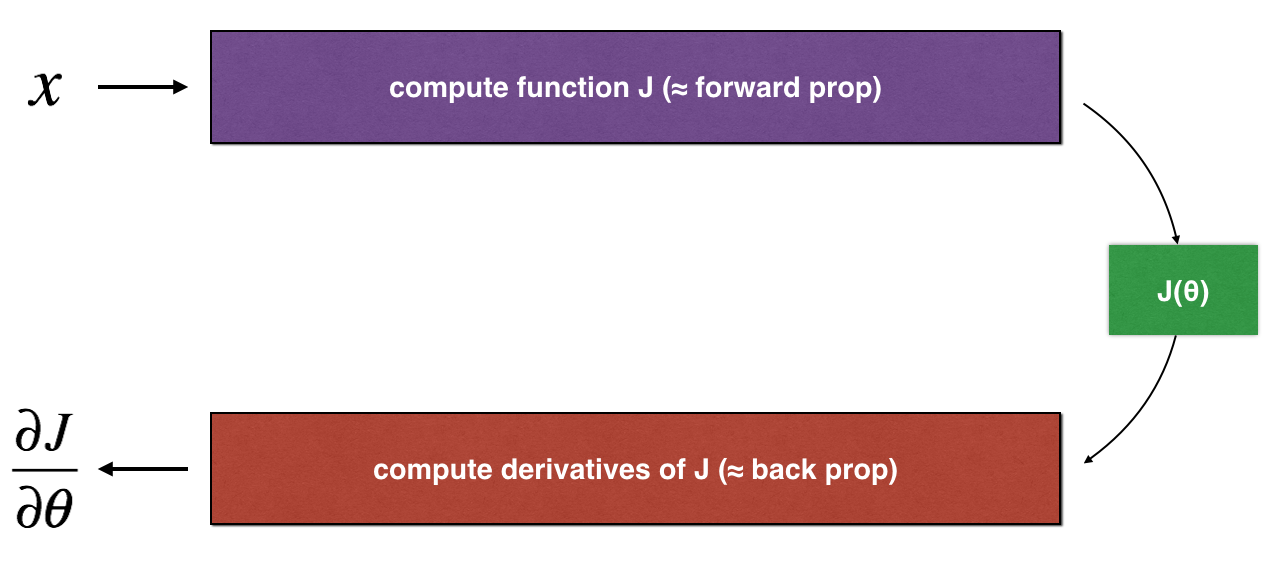
上图显示了关键的计算步骤: 首先输入 \(x\), 接着计算代价函数 \(J(x)\) ("正传"). 最后计算 \(\frac{\partial J}{\partial \theta}\) ("b反传").

1
2
3
4
# Packages
import numpy as np
from testCases import *
from gc_utils import sigmoid, relu, dictionary_to_vector, vector_to_dictionary, gradients_to_vector
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# GRADED FUNCTION: forward_propagation

def forward_propagation(x, theta):
    """
    Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x)
    
    Arguments:
    x -- a real-valued input
    theta -- our parameter, a real number as well
    
    Returns:
    J -- the value of function J, computed using the formula J(theta) = theta * x
    """
    
    ### START CODE HERE ### (approx. 1 line)
    J = theta * x
    ### END CODE HERE ###
    
    return J
1
2
3
x, theta = 2, 4
J = forward_propagation(x, theta)
print ("J = " + str(J))
J = 8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# GRADED FUNCTION: backward_propagation

def backward_propagation(x, theta):
    """
    Computes the derivative of J with respect to theta (see Figure 1).
    
    Arguments:
    x -- a real-valued input
    theta -- our parameter, a real number as well
    
    Returns:
    dtheta -- the gradient of the cost with respect to theta
    """
    
    ### START CODE HERE ### (approx. 1 line)
    dtheta = x
    ### END CODE HERE ###
    
    return dtheta
1
2
3
x, theta = 2, 4
dtheta = backward_propagation(x, theta)
print ("dtheta = " + str(dtheta))
dtheta = 2

梯度验证步骤: - 首先利用公式（1）和一个小值 \(\varepsilon\)计算"gradapprox"，具体的步骤包括: 1. \(\theta^{+} = \theta + \varepsilon\) 2. \(\theta^{-} = \theta - \varepsilon\) 3. \(J^{+} = J(\theta^{+})\) 4. \(J^{-} = J(\theta^{-})\) 5. \(gradapprox = \frac{J^{+} - J^{-}}{2 \varepsilon}\) - 利用反传函数计算 "grad" - 最后计算"gradapprox" 和"grad" 的差异: \[ difference = \frac {\mid\mid grad - gradapprox \mid\mid_2}{\mid\mid grad \mid\mid_2 + \mid\mid gradapprox \mid\mid_2} \tag{2}\] - 当差异很小时 (比如小于 \(10^{-7}\)), 则梯度计算正确，否则，梯度计算可能存在问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# GRADED FUNCTION: gradient_check

def gradient_check(x, theta, epsilon = 1e-7):
    """
    Implement the backward propagation presented in Figure 1.
    
    Arguments:
    x -- a real-valued input
    theta -- our parameter, a real number as well
    epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
    
    Returns:
    difference -- difference (2) between the approximated gradient and the backward propagation gradient
    """
    
    # Compute gradapprox using left side of formula (1). epsilon is small enough, you don't need to worry about the limit.
    ### START CODE HERE ### (approx. 5 lines)
    thetaplus = theta + epsilon                               # Step 1
    thetaminus = theta - epsilon                              # Step 2
    J_plus = forward_propagation(x, thetaplus)                                  # Step 3
    J_minus = forward_propagation(x, thetaminus)                                 # Step 4
    gradapprox = (J_plus - J_minus) / ( 2. * epsilon)                             # Step 5
    ### END CODE HERE ###
    
    # Check if gradapprox is close enough to the output of backward_propagation()
    ### START CODE HERE ### (approx. 1 line)
    grad = backward_propagation(x, theta)
    ### END CODE HERE ###
        
    ### START CODE HERE ### (approx. 1 line)
    numerator = np.linalg.norm(grad - gradapprox)                               # Step 1'
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)                             # Step 2'
    difference = numerator / denominator                              # Step 3'
    ### END CODE HERE ###
    
    if difference < 1e-7:
        print ("The gradient is correct!")
    else:
        print ("The gradient is wrong!")
    
    return difference
1
2
3
x, theta = 2, 4
difference = gradient_check(x, theta)
print("difference = " + str(difference))
The gradient is correct!
difference = 2.91933588329e-10

N维梯度验证

图 2 : 深度神经网络
LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def forward_propagation_n(X, Y, parameters):
    """
    Implements the forward propagation (and computes the cost) presented in Figure 3.
    
    Arguments:
    X -- training set for m examples
    Y -- labels for m examples 
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
                    W1 -- weight matrix of shape (5, 4)
                    b1 -- bias vector of shape (5, 1)
                    W2 -- weight matrix of shape (3, 5)
                    b2 -- bias vector of shape (3, 1)
                    W3 -- weight matrix of shape (1, 3)
                    b3 -- bias vector of shape (1, 1)
    
    Returns:
    cost -- the cost function (logistic cost for one example)
    """
    
    # retrieve parameters
    m = X.shape[1]
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]

    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    Z1 = np.dot(W1, X) + b1
    A1 = relu(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = relu(Z2)
    Z3 = np.dot(W3, A2) + b3
    A3 = sigmoid(Z3)

    # Cost
    logprobs = np.multiply(-np.log(A3),Y) + np.multiply(-np.log(1 - A3), 1 - Y)
    cost = 1./m * np.sum(logprobs)
    
    cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
    
    return cost, cache
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def backward_propagation_n(X, Y, cache):
    """
    Implement the backward propagation presented in figure 2.
    
    Arguments:
    X -- input datapoint, of shape (input size, 1)
    Y -- true "label"
    cache -- cache output from forward_propagation_n()
    
    Returns:
    gradients -- A dictionary with the gradients of the cost with respect to each parameter, activation and pre-activation variables.
    """
    
    m = X.shape[1]
    (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
    
    dZ3 = A3 - Y
    dW3 = 1./m * np.dot(dZ3, A2.T)
    db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
    
    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2 > 0))
    dW2 = 1./m * np.dot(dZ2, A1.T)
    db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
    
    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1 > 0))
    dW1 = 1./m * np.dot(dZ1, X.T)
    db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
    
    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
                 "dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
                 "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
    
    return gradients

梯度验证步骤:

和一维梯度验证类似，需要对比"gradapprox" 和反传函数计算的梯度:

\[ \frac{\partial J}{\partial \theta} = \lim_{\varepsilon \to 0} \frac{J(\theta + \varepsilon) - J(\theta - \varepsilon)}{2 \varepsilon} \tag{1}\]

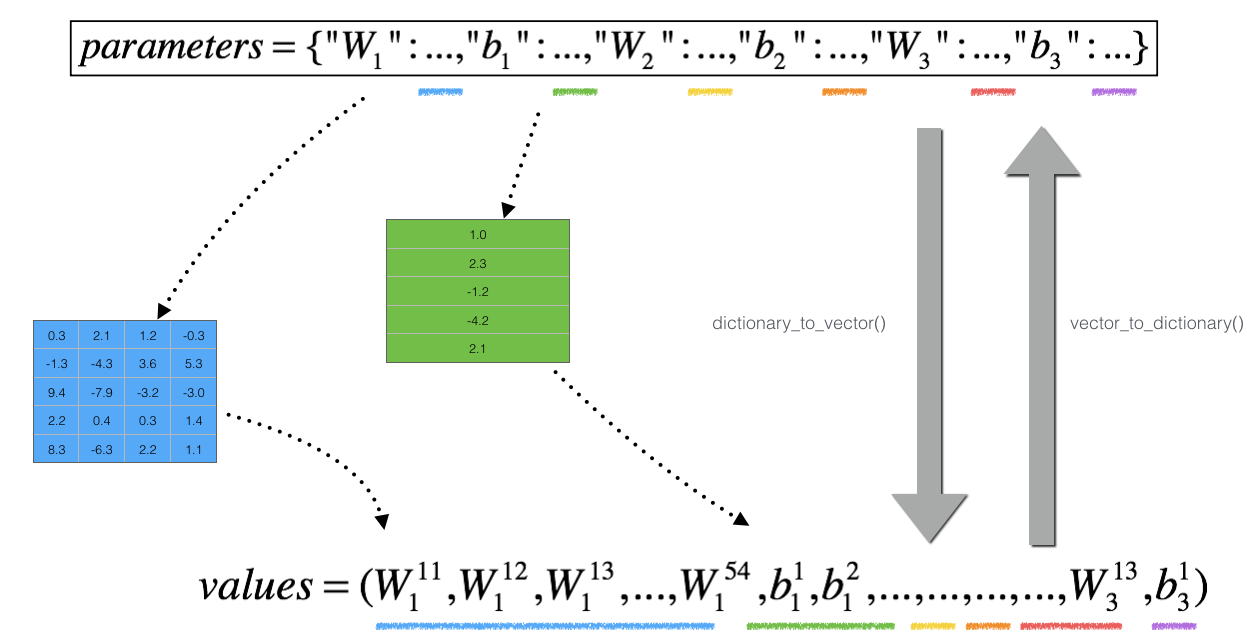
但是, \(\theta\) 不再是标量，而是一个字典"parameters". 此处提供了 "dictionary_to_vector()"，它将字典 "parameters" 转化成向量 "values"。

逆过程为"vector_to_dictionary"输出字典 "parameters".

图 2 : dictionary_to_vector() and vector_to_dictionary()

循环num_parameters个参数: - 计算J_plus[i]: 1. 令 \(\theta^{+}\) 为 np.copy(parameters_values) 2. 令 \(\theta^{+}_i\) 为 \(\theta^{+}_i + \varepsilon\) 3. 利用函数forward_propagation_n(x, y, vector_to_dictionary(\(\theta^{+}\) ))计算 \(J^{+}_i\) .
- 用相同的方法计算\(\theta^{-}\)的J_minus[i] - 计算 \(gradapprox[i] = \frac{J^{+}_i - J^{-}_i}{2 \varepsilon}\)

因此可以得到向量 gradapprox, 其中 gradapprox[i] 为相对于参数 parameter_values[i]的梯度近似结果. 将其对比反传函数计算的梯度向量. 和1D 情况下类似，计算: \[ difference = \frac {\| grad - gradapprox \|_2}{\| grad \|_2 + \| gradapprox \|_2 } \tag{3}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
# GRADED FUNCTION: gradient_check_n

def gradient_check_n(parameters, gradients, X, Y, epsilon = 1e-7):
    """
    Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
    
    Arguments:
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
    grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters. 
    x -- input datapoint, of shape (input size, 1)
    y -- true "label"
    epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
    
    Returns:
    difference -- difference (2) between the approximated gradient and the backward propagation gradient
    """
    
    # Set-up variables
    parameters_values, _ = dictionary_to_vector(parameters)
    grad = gradients_to_vector(gradients)
    num_parameters = parameters_values.shape[0]
    J_plus = np.zeros((num_parameters, 1))
    J_minus = np.zeros((num_parameters, 1))
    gradapprox = np.zeros((num_parameters, 1))
    
    # Compute gradapprox
    for i in range(num_parameters):
        
        # Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]".
        # "_" is used because the function you have to outputs two parameters but we only care about the first one
        ### START CODE HERE ### (approx. 3 lines)
        thetaplus = np.copy(parameters_values)                                      # Step 1
        thetaplus[i][0] += epsilon
        # Step 2
        J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaplus))                                   # Step 3
        ### END CODE HERE ###
        
        # Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]".
        ### START CODE HERE ### (approx. 3 lines)
        thetaminus = np.copy(parameters_values)                                     # Step 1
        thetaminus[i][0] -= epsilon                               # Step 2        
        J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaminus))                                  # Step 3
        ### END CODE HERE ###
        
        # Compute gradapprox[i]
        ### START CODE HERE ### (approx. 1 line)
        gradapprox[i] = (J_plus[i] - J_minus[i]) / (2. * epsilon)
        ### END CODE HERE ###
    
    # Compare gradapprox to backward propagation gradients by computing difference.
    ### START CODE HERE ### (approx. 1 line)
    numerator = np.linalg.norm(grad - gradapprox)                               # Step 1'
    denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)             # Step 2'
    difference = numerator / denominator  

    if difference > 1e-7:
        print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
    else:
        print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
    
    return difference
1
2
3
4
5
X, Y, parameters = gradient_check_n_test_case()

cost, cache = forward_propagation_n(X, Y, parameters)
gradients = backward_propagation_n(X, Y, cache)
difference = gradient_check_n(parameters, gradients, X, Y)
There is a mistake in the backward propagation! difference = 1.18904178788e-07

结论

  1. 梯度验证十分耗时，因此不会在训练的每一次迭代都进行梯度验证，而是只做几次验证
  2. 梯度验证不能和dropout一起使用，一般是在使用dropout之前保证梯度是正确的，然后再将dropout加进去

参考资料