Tensorflow简单教程

发表于 | 分类于

本文介绍一种十分通用的深度学习编程框架：Tensorflow。该变成框架主要包含两个对象：张量和操作。通过这两个对象可以建立一个计算图，再启动会话以执行该计算图。对深度神经网络应用来说，只需要在会话中运行“optimizer”对象，Tensoflow就可以自动运行反传和模型更新，十分便捷。

基本用法

对单个样本，计算代价函数： \[loss = \mathcal{L}(\hat{y}, y) = (\hat y^{(i)} - y^{(i)})^2 \tag{1}\]

1
2
3
4
5
6
7
8
9
10
import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.python.framework import ops
from tf_utils import load_dataset, random_mini_batches, convert_to_one_hot, predict

%matplotlib inline
np.random.seed(1)
1
2
3
4
5
6
7
8
9
10
y_hat = tf.constant(36, name='y_hat')            # Define y_hat constant. Set to 36.
y = tf.constant(39, name='y')                    # Define y. Set to 39

loss = tf.Variable((y - y_hat)**2, name='loss')  # Create a variable for the loss

init = tf.global_variables_initializer()         # When init is run later (session.run(init)),
                                                 # the loss variable will be initialized and ready to be computed
with tf.Session() as session:                    # Create a session and print the output
    session.run(init)                            # Initializes the variables
    print(session.run(loss))                     # Prints the loss
9

在Tensorflow下编写和运行程序有以下几步：

  1. 建立张量或变量
  2. 编写张量之间的操作
  3. 初始化张量
  4. 建立一个session
  5. 运行这个session，此时会执行前面编写的操作
1
2
3
4
a = tf.constant(2)
b = tf.constant(10)
c = tf.multiply(a,b)
print(c)
Tensor("Mul:0", shape=(), dtype=int32)

从上面可以看出，你并没有看到20，而是输出一个没有维度信息的张量。上面的语句只是把操作放进了“运算图”中，并没有执行运算。为了执行运算，需要建立一个session，然后运行这个session。

1
2
sess = tf.Session()
print(sess.run(c))
20

下面介绍placeholder的用法，placeholder是一个对象，它的值可以稍后指定。为了对这个placeholder设定值，可以使用"feed dictionary"(变量feed_dict)。下面是一个简单的例子:

1
2
3
4
5
# Change the value of x in the feed_dict

x = tf.placeholder(tf.int64, name = 'x')
print(sess.run(2 * x, feed_dict = {x: 3}))
sess.close()
6

线性函数

计算 \(Y = WX + b\), 其中 \(W\) 和 \(X\) 都是随机向量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# GRADED FUNCTION: linear_function

def linear_function():
    """
    Implements a linear function: 
            Initializes W to be a random tensor of shape (4,3)
            Initializes X to be a random tensor of shape (3,1)
            Initializes b to be a random tensor of shape (4,1)
    Returns: 
    result -- runs the session for Y = WX + b 
    """
    
    np.random.seed(1)
    
    ### START CODE HERE ### (4 lines of code)
    X = tf.constant(np.random.randn(3, 1), name='X')
    W = tf.constant(np.random.randn(4, 3), name='W')
    b = tf.constant(np.random.randn(4, 1), name='b')
    Y = tf.add(tf.matmul(W, X), b)
    ### END CODE HERE ### 
    
    # Create the session using tf.Session() and run it with sess.run(...) on the variable you want to calculate
    
    ### START CODE HERE ###
    sess = tf.Session()
    result = sess.run(Y)
    ### END CODE HERE ### 
    
    # close the session 
    sess.close()

    return result
1
print( "result = " + str(linear_function()))
result = [[-2.15657382]
 [ 2.95891446]
 [-1.08926781]
 [-0.84538042]]

计算sigmoid函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# GRADED FUNCTION: sigmoid

def sigmoid(z):
    """
    Computes the sigmoid of z
    
    Arguments:
    z -- input value, scalar or vector
    
    Returns: 
    results -- the sigmoid of z
    """
    
    ### START CODE HERE ### ( approx. 4 lines of code)
    # Create a placeholder for x. Name it 'x'.
    x = tf.placeholder(tf.float32, name='x')

    # compute sigmoid(x)
    sigmoid = tf.sigmoid(x)

    # Create a session, and run it. Please use the method 2 explained above. 
    # You should use a feed_dict to pass z's value to x. 
    with tf.Session() as sess:
        # Run session and call the output "result"
        result = sess.run(sigmoid, feed_dict={x: z})
    
    ### END CODE HERE ###
    
    return result
1
2
print ("sigmoid(0) = " + str(sigmoid(0)))
print ("sigmoid(12) = " + str(sigmoid(12)))
sigmoid(0) = 0.5
sigmoid(12) = 0.999994

计算代价函数

对2层神经网络，代价函数是 \(a^{[2](i)}\) 和 \(y^{(i)}\)的函数， for i=1...m: \[ J = - \frac{1}{m} \sum_{i = 1}^m \large ( \small y^{(i)} \log a^{ [2] (i)} + (1-y^{(i)})\log (1-a^{ [2] (i)} )\large )\small\tag{2}\]

Tensoflow只需要一行代码 - tf.nn.sigmoid_cross_entropy_with_logits(logits = ..., labels = ...) 计算的是： \[- \frac{1}{m} \sum_{i = 1}^m \large ( \small y^{(i)} \log \sigma(z^{[2](i)}) + (1-y^{(i)})\log (1-\sigma(z^{[2](i)})\large )\small\tag{2}\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# GRADED FUNCTION: cost

def cost(logits, labels):
    """
    Computes the cost using the sigmoid cross entropy
    
    Arguments:
    logits -- vector containing z, output of the last linear unit (before the final sigmoid activation)
    labels -- vector of labels y (1 or 0) 
    
    Note: What we've been calling "z" and "y" in this class are respectively called "logits" and "labels" 
    in the TensorFlow documentation. So logits will feed into z, and labels into y. 
    
    Returns:
    cost -- runs the session of the cost (formula (2))
    """
    
    ### START CODE HERE ### 
    
    # Create the placeholders for "logits" (z) and "labels" (y) (approx. 2 lines)
    z = tf.placeholder(tf.float32, name='z')
    y = tf.placeholder(tf.float32, name='y')
    
    # Use the loss function (approx. 1 line)
    cost = tf.nn.sigmoid_cross_entropy_with_logits(logits=z, labels=y)
    
    # Create a session (approx. 1 line). See method 1 above.
    sess = tf.Session()
    
    # Run the session (approx. 1 line).
    cost = sess.run(cost, feed_dict={z: logits, y:labels})
    
    # Close the session (approx. 1 line). See method 1 above.
    sess.close()
    
    ### END CODE HERE ###
    
    return cost
1
2
3
logits = sigmoid(np.array([0.2,0.4,0.7,0.9]))
cost = cost(logits, np.array([0,0,1,1]))
print ("cost = " + str(cost))
cost = [ 1.00538719  1.03664088  0.41385433  0.39956614]

One Hot编码

在深度学习中，经常会有向量y从 0 到 C-1变化, 其中 C 是类别数.如果C 为4的话，需要转化成下面的形式：:

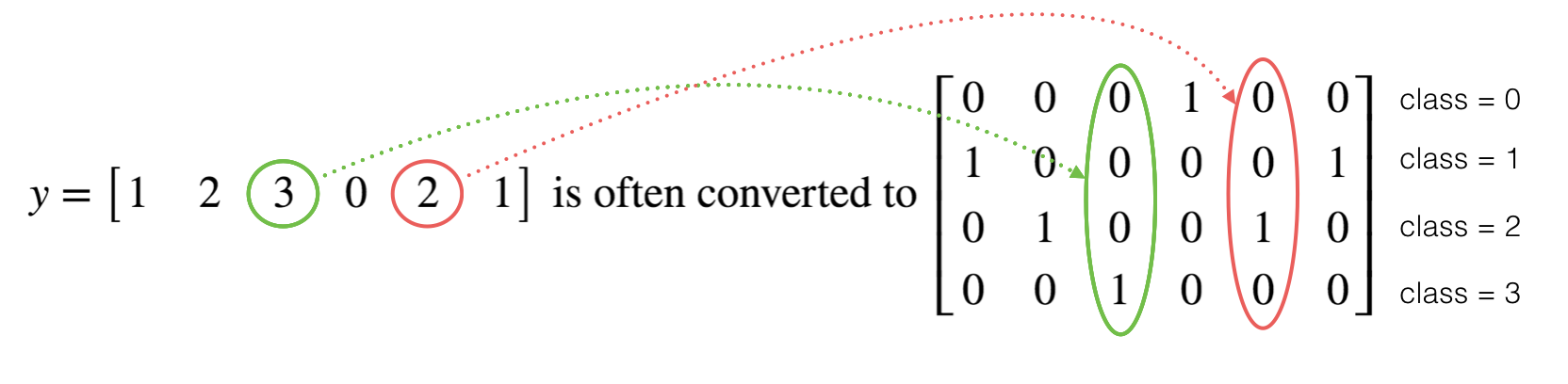
上面称为"one hot" 编码, 这个名字起源于每一列只有一个元素是热点（为1）. 为实现这个功能，numpy可能需要几行代码，而tensorflow只需要一行,:

  • tf.one_hot(labels, depth, axis)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# GRADED FUNCTION: one_hot_matrix

def one_hot_matrix(labels, C):
    """
    Creates a matrix where the i-th row corresponds to the ith class number and the jth column
                     corresponds to the jth training example. So if example j had a label i. Then entry (i,j) 
                     will be 1. 
                     
    Arguments:
    labels -- vector containing the labels 
    C -- number of classes, the depth of the one hot dimension
    
    Returns: 
    one_hot -- one hot matrix
    """
    
    ### START CODE HERE ###
    
    # Create a tf.constant equal to C (depth), name it 'C'. (approx. 1 line)
    C = tf.constant(C, name='C')
    
    # Use tf.one_hot, be careful with the axis (approx. 1 line)
    one_hot_matrix = tf.one_hot(indices=labels, depth=C, axis=0)
    
    # Create the session (approx. 1 line)
    sess = tf.Session()
    
    # Run the session (approx. 1 line)
    one_hot = sess.run(one_hot_matrix)
    
    # Close the session (approx. 1 line). See method 1 above.
    sess.close()
    
    ### END CODE HERE ###
    
    return one_hot
1
2
3
labels = np.array([1,2,3,0,2,1])
one_hot = one_hot_matrix(labels, C = 4)
print ("one_hot = " + str(one_hot))
one_hot = [[ 0.  0.  0.  1.  0.  0.]
 [ 1.  0.  0.  0.  0.  1.]
 [ 0.  1.  0.  0.  1.  0.]
 [ 0.  0.  1.  0.  0.  0.]]

初始化0和1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# GRADED FUNCTION: ones

def ones(shape):
    """
    Creates an array of ones of dimension shape
    
    Arguments:
    shape -- shape of the array you want to create
        
    Returns: 
    ones -- array containing only ones
    """
    
    ### START CODE HERE ###
    
    # Create "ones" tensor using tf.ones(...). (approx. 1 line)
    ones = tf.ones(shape)
    
    # Create the session (approx. 1 line)
    sess = tf.Session()
    
    # Run the session to compute 'ones' (approx. 1 line)
    ones = sess.run(ones)
    
    # Close the session (approx. 1 line). See method 1 above.
    sess.close()
    
    ### END CODE HERE ###
    return ones
1
print ("ones = " + str(ones([3])))
ones = [ 1.  1.  1.]

建立第一个神经网络

  • 训练集: 1080 张代表0-5的图 (64 × 64) (每个数字180 张图).
  • 测试集: 120 张代表0-5的图 (64 × 64 )(每个数字20 张图).
Figure 1: SIGNS dataset 
1
2
# Loading the dataset
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()
1
2
3
4
# Example of a picture
index = 0
plt.imshow(X_train_orig[index])
print ("y = " + str(np.squeeze(Y_train_orig[:, index])))
y = 5
png

png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Flatten the training and test images
X_train_flatten = X_train_orig.reshape(X_train_orig.shape[0], -1).T
X_test_flatten = X_test_orig.reshape(X_test_orig.shape[0], -1).T
# Normalize image vectors
X_train = X_train_flatten/255.
X_test = X_test_flatten/255.
# Convert training and test labels to one hot matrices
Y_train = convert_to_one_hot(Y_train_orig, 6)
Y_test = convert_to_one_hot(Y_test_orig, 6)

print ("number of training examples = " + str(X_train.shape[1]))
print ("number of test examples = " + str(X_test.shape[1]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
number of training examples = 1080
number of test examples = 120
X_train shape: (12288, 1080)
Y_train shape: (6, 1080)
X_test shape: (12288, 120)
Y_test shape: (6, 120)

模型：LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAX. 与二分类使用 SIGMOID 作为输出层不同， 多分类问题使用 SOFTMAX.

建立占位符

首先建立X和Y的占位符，然后在运行会话时，将训练数据集传进占位符。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# GRADED FUNCTION: create_placeholders

def create_placeholders(n_x, n_y):
    """
    Creates the placeholders for the tensorflow session.
    
    Arguments:
    n_x -- scalar, size of an image vector (num_px * num_px = 64 * 64 * 3 = 12288)
    n_y -- scalar, number of classes (from 0 to 5, so -> 6)
    
    Returns:
    X -- placeholder for the data input, of shape [n_x, None] and dtype "float"
    Y -- placeholder for the input labels, of shape [n_y, None] and dtype "float"
    
    Tips:
    - You will use None because it let's us be flexible on the number of examples you will for the placeholders.
      In fact, the number of examples during test/train is different.
    """

    ### START CODE HERE ### (approx. 2 lines)
    X = tf.placeholder(tf.float32, shape=[n_x, None], name='X')
    Y = tf.placeholder(tf.float32, shape=[n_y, None], name='Y')
    ### END CODE HERE ###
    
    return X, Y
1
2
3
X, Y = create_placeholders(12288, 6)
print ("X = " + str(X))
print ("Y = " + str(Y))
X = Tensor("X_1:0", shape=(12288, ?), dtype=float32)
Y = Tensor("Y:0", shape=(6, ?), dtype=float32)

参数初始化

采用Xavier初始化权系数，零初始化偏置量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# GRADED FUNCTION: initialize_parameters

def initialize_parameters():
    """
    Initializes parameters to build a neural network with tensorflow. The shapes are:
                        W1 : [25, 12288]
                        b1 : [25, 1]
                        W2 : [12, 25]
                        b2 : [12, 1]
                        W3 : [6, 12]
                        b3 : [6, 1]
    
    Returns:
    parameters -- a dictionary of tensors containing W1, b1, W2, b2, W3, b3
    """
    
    tf.set_random_seed(1)                   # so that your "random" numbers match ours
        
    ### START CODE HERE ### (approx. 6 lines of code)
    W1 = tf.get_variable("W1", [25, 12288], initializer=tf.contrib.layers.xavier_initializer(seed=1))
    b1 = tf.get_variable("b1", [25, 1], initializer=tf.zeros_initializer())
    W2 = tf.get_variable("W2", [12, 25], initializer=tf.contrib.layers.xavier_initializer(seed=1))
    b2 = tf.get_variable("b2", [12, 1], initializer=tf.zeros_initializer())
    W3 = tf.get_variable("W3", [6, 12], initializer=tf.contrib.layers.xavier_initializer(seed=1))
    b3 = tf.get_variable("b3", [6, 1], initializer=tf.zeros_initializer())
    ### END CODE HERE ###

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2,
                  "W3": W3,
                  "b3": b3}
    
    return parameters
1
2
3
4
5
6
7
tf.reset_default_graph()
with tf.Session() as sess:
    parameters = initialize_parameters()
    print("W1 = " + str(parameters["W1"]))
    print("b1 = " + str(parameters["b1"]))
    print("W2 = " + str(parameters["W2"]))
    print("b2 = " + str(parameters["b2"]))
W1 = <tf.Variable 'W1:0' shape=(25, 12288) dtype=float32_ref>
b1 = <tf.Variable 'b1:0' shape=(25, 1) dtype=float32_ref>
W2 = <tf.Variable 'W2:0' shape=(12, 25) dtype=float32_ref>
b2 = <tf.Variable 'b2:0' shape=(12, 1) dtype=float32_ref>

正传播

需要注意的是，和之前使用numpy实现正传不同，tensorflow的线性层最终输出为z3，这是因为最后要使用z3作为输入计算代价函数，所以不需要提前计算a3。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# GRADED FUNCTION: forward_propagation

def forward_propagation(X, parameters):
    """
    Implements the forward propagation for the model: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAX
    
    Arguments:
    X -- input dataset placeholder, of shape (input size, number of examples)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3"
                  the shapes are given in initialize_parameters

    Returns:
    Z3 -- the output of the last LINEAR unit
    """
    
    # Retrieve the parameters from the dictionary "parameters" 
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    W3 = parameters['W3']
    b3 = parameters['b3']
    
    ### START CODE HERE ### (approx. 5 lines)              # Numpy Equivalents:
    Z1 = tf.add(tf.matmul(W1, X), b1)                                             # Z1 = np.dot(W1, X) + b1
    A1 = tf.nn.relu(Z1)                                              # A1 = relu(Z1)
    Z2 = tf.add(tf.matmul(W2, A1), b2)                                              # Z2 = np.dot(W2, a1) + b2
    A2 = tf.nn.relu(Z2)                                              # A2 = relu(Z2)
    Z3 = tf.add(tf.matmul(W3, A2), b3)                                              # Z3 = np.dot(W3,Z2) + b3
    ### END CODE HERE ###
    
    return Z3
1
2
3
4
5
6
7
tf.reset_default_graph()

with tf.Session() as sess:
    X, Y = create_placeholders(12288, 6)
    parameters = initialize_parameters()
    Z3 = forward_propagation(X, parameters)
    print("Z3 = " + str(Z3))
Z3 = Tensor("Add_2:0", shape=(6, ?), dtype=float32)

计算代价函数

需要注意的是，tensorflow中只需要一行代码计算： 

1
tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = ..., labels = ...))

但是需要"logits" 和 "labels"的输入维度是(样本数, 分类数)。另外tf.reduce_mean是对所有样本求和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# GRADED FUNCTION: compute_cost 

def compute_cost(Z3, Y):
    """
    Computes the cost
    
    Arguments:
    Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)
    Y -- "true" labels vector placeholder, same shape as Z3
    
    Returns:
    cost - Tensor of the cost function
    """
    
    # to fit the tensorflow requirement for tf.nn.softmax_cross_entropy_with_logits(...,...)
    logits = tf.transpose(Z3)
    labels = tf.transpose(Y)
    
    ### START CODE HERE ### (1 line of code)
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits,
                                                                 labels=labels))
    ### END CODE HERE ###
    
    return cost
1
2
3
4
5
6
7
8
tf.reset_default_graph()

with tf.Session() as sess:
    X, Y = create_placeholders(12288, 6)
    parameters = initialize_parameters()
    Z3 = forward_propagation(X, parameters)
    cost = compute_cost(Z3, Y)
    print("cost = " + str(cost))
cost = Tensor("Mean:0", shape=(), dtype=float32)

反传及参数更新

这是使用编程框架的优势所在，所有的反传和模型更新只需要几行代码。

计算代价函数之后，就可以建立一个“优化”对象。在会话开始运行之后，调用这个对象，就会根据选择的优化方法和学习率优化这个目标函数

例如，使用梯度下降法： 

1
optimizer = tf.train.GradientDescentOptimizer(learning_rate = learning_rate).minimize(cost)

运行优化算法： 

1
_ , c = sess.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})

上面的语句则会实现反传及参数更新。

建立模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.0001,
          num_epochs = 1500, minibatch_size = 32, print_cost = True):
    """
    Implements a three-layer tensorflow neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SOFTMAX.
    
    Arguments:
    X_train -- training set, of shape (input size = 12288, number of training examples = 1080)
    Y_train -- test set, of shape (output size = 6, number of training examples = 1080)
    X_test -- training set, of shape (input size = 12288, number of training examples = 120)
    Y_test -- test set, of shape (output size = 6, number of test examples = 120)
    learning_rate -- learning rate of the optimization
    num_epochs -- number of epochs of the optimization loop
    minibatch_size -- size of a minibatch
    print_cost -- True to print the cost every 100 epochs
    
    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
    """
    
    ops.reset_default_graph()                         # to be able to rerun the model without overwriting tf variables
    tf.set_random_seed(1)                             # to keep consistent results
    seed = 3                                          # to keep consistent results
    (n_x, m) = X_train.shape                          # (n_x: input size, m : number of examples in the train set)
    n_y = Y_train.shape[0]                            # n_y : output size
    costs = []                                        # To keep track of the cost
    
    # Create Placeholders of shape (n_x, n_y)
    ### START CODE HERE ### (1 line)
    X, Y = create_placeholders(n_x, n_y)
    ### END CODE HERE ###

    # Initialize parameters
    ### START CODE HERE ### (1 line)
    parameters = initialize_parameters()
    ### END CODE HERE ###
    
    # Forward propagation: Build the forward propagation in the tensorflow graph
    ### START CODE HERE ### (1 line)
    Z3 = forward_propagation(X, parameters)
    ### END CODE HERE ###
    
    # Cost function: Add cost function to tensorflow graph
    ### START CODE HERE ### (1 line)
    cost = compute_cost(Z3, Y)
    ### END CODE HERE ###
    
    # Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer.
    ### START CODE HERE ### (1 line)
    optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
    ### END CODE HERE ###
    
    # Initialize all the variables
    init = tf.global_variables_initializer()

    # Start the session to compute the tensorflow graph
    with tf.Session() as sess:
        
        # Run the initialization
        sess.run(init)
        
        # Do the training loop
        for epoch in range(num_epochs):

            epoch_cost = 0.                       # Defines a cost related to an epoch
            num_minibatches = int(m / minibatch_size) # number of minibatches of size minibatch_size in the train set
            seed = seed + 1
            minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)

            for minibatch in minibatches:

                # Select a minibatch
                (minibatch_X, minibatch_Y) = minibatch
                
                # IMPORTANT: The line that runs the graph on a minibatch.
                # Run the session to execute the "optimizer" and the "cost", the feedict should contain a minibatch for (X,Y).
                ### START CODE HERE ### (1 line)
                _ , minibatch_cost = sess.run([optimizer, cost], 
                                             feed_dict={X: minibatch_X, 
                                                        Y: minibatch_Y})
                ### END CODE HERE ###
                
                epoch_cost += minibatch_cost / num_minibatches

            # Print the cost every epoch
            if print_cost == True and epoch % 100 == 0:
                print ("Cost after epoch %i: %f" % (epoch, epoch_cost))
            if print_cost == True and epoch % 5 == 0:
                costs.append(epoch_cost)
                
        # plot the cost
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()

        # lets save the parameters in a variable
        parameters = sess.run(parameters)
        print ("Parameters have been trained!")

        # Calculate the correct predictions
        correct_prediction = tf.equal(tf.argmax(Z3), tf.argmax(Y))

        # Calculate accuracy on the test set
        accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

        print ("Train Accuracy:", accuracy.eval({X: X_train, Y: Y_train}))
        print ("Test Accuracy:", accuracy.eval({X: X_test, Y: Y_test}))
        
        return parameters
1
parameters = model(X_train, Y_train, X_test, Y_test)
Cost after epoch 0: 1.855702
Cost after epoch 100: 1.016458
Cost after epoch 200: 0.733102
Cost after epoch 300: 0.572940
Cost after epoch 400: 0.468774
Cost after epoch 500: 0.381021
Cost after epoch 600: 0.313822
Cost after epoch 700: 0.254158
Cost after epoch 800: 0.203829
Cost after epoch 900: 0.166421
Cost after epoch 1000: 0.141486
Cost after epoch 1100: 0.107580
Cost after epoch 1200: 0.086270
Cost after epoch 1300: 0.059371
Cost after epoch 1400: 0.052228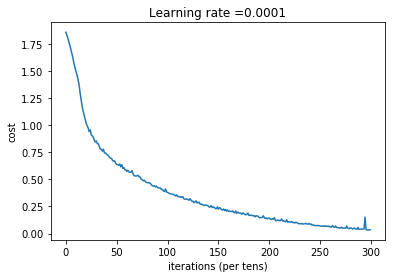
png

png

Parameters have been trained!
Train Accuracy: 0.999074
Test Accuracy: 0.716667

小结：模型过拟合，可以采用L2正则化或者dropout方法缓解过拟合问题

测试用户的图像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import scipy
from PIL import Image
from scipy import ndimage

## START CODE HERE ## (PUT YOUR IMAGE NAME) 
my_image = "thumbs_up.jpg"
## END CODE HERE ##

# We preprocess your image to fit your algorithm.
fname = "images/" + my_image
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(64,64)).reshape((1, 64*64*3)).T
my_image_prediction = predict(my_image, parameters)

plt.imshow(image)
print("Your algorithm predicts: y = " + str(np.squeeze(my_image_prediction)))
Your algorithm predicts: y = 3
png

png

小结：上面的测试数据分类错误，这是因为训练数据集中没有这样的数据，于是出现了数据分布不匹配的问题。这是深度学习中一个非常经典的问题。

结论

  1. Tensorflow是一种广泛使用的深度学习编程框架，它主要包含两个对象类：张量和操作
  2. 使用Tensorflow必须遵循这样几步：
  • 建立计算图，包括张量（变量、占位符等）和操作（加法、乘法等）
  • 建立一个会话
  • 初始化会话
  • 运行会话以执行计算图
  1. 计算图可以执行多次，如model()函数所示
  2. 在Tensorflow中，当运行“optimizer”对象之后，反传和模型更新是自动运行的。

参考资料