线性回归

发表于 | 分类于

线性回归是机器学习中最为重要的算法之一，简单高效，也是神经网络等非线性模型的基础。本文介绍线性回归、局部加权线性回归、L2/L1约束下回归（分别叫岭回归和Lasso回归），并引用MLiA一书中的程序和例子介绍算法细节和应用场景。

基本原理及算法

线性回归

原问题可描述为： \[ f(\mathbf{x}_i) = \mathbf{w}^T \mathbf{x}_i + b \] 使得 \[ f(\mathbf{x}_i) \approx y_i \] 将截距b吸收入向量\(\hat{\mathbf{w}} = (\mathbf{w};b)\)，简化为\(\mathbf{w}\)。把数据集表示为\(m*(d+1)\)大小的矩阵，每行对应一个样本，一行中前\(d\)个元素对应于样本的第\(d\)个属性，最后一个元素恒为1，则原问题可以表述为求解以下反问题: \[ \mathbf{w}^* = argmin_{\mathbf{w}} (\mathbf{y} - \mathbf{X} \mathbf{w})^T ( \mathbf{y} - \mathbf{X} \mathbf{w}) \] 当\(\mathbf{X}^T\mathbf{X}\)为满秩矩阵时： \[ \mathbf{w}^* = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \mathbf{y} \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from numpy import *
def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t')) # 列数作为特征数，包括标签，最后会排除最后一列
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat - 1):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1])) # 最后一列为标签
    return dataMat, labelMat

def standRegres(xArr, yArr):
    """
    标准的线性回归算法
    xArr: (m, n)
    yArr: (1, m)
    输出ws: (n, 1)
    """
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat
    if linalg.det(xTx) == 0.0:
        print("Matrix is singular")
        return
    ws = xTx.I * (xMat.T*yMat)
    return ws
1
2
3
xArr, yArr = loadDataSet('ex0.txt')
ws = standRegres(xArr, yArr)
ws
matrix([[ 3.00774324],
        [ 1.69532264]])
1
2
3
4
5
6
7
8
9
10
11
12
# 绘制数据点及最佳拟合直线
import matplotlib.pyplot as plt
xMat = mat(xArr)
yMat = mat(yArr)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xMat[:,1].flatten().A[0], yMat.T[:,0].flatten().A[0])
xCopy = xMat.copy()
xCopy.sort(0)
yHat = xCopy*ws
ax.plot(xCopy[:,1],yHat)
plt.show()
png

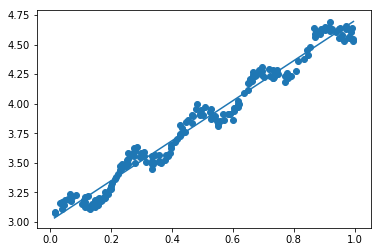
png

局部加权线性回归

线性回归很容易出现欠拟合现象，一种办法是局部加权线性回归(LWLR: Locally Weighted Linear Regression)。在该方法中，给待预测点附近的每个样点赋予一定的权重。 \[ \mathbf{w}^* = (\mathbf{X}^T \mathbf{W} \mathbf{X})^{-1} \mathbf{X}^T \mathbf{W} \mathbf{y} \] LWLR使用核方法的思想对附近点赋予更高的权重，核的类型可以自由选择，最常用的是高斯核，对应的公式为： \[ w(i) = exp \left ( -\frac{\|\mathbf{x}_{i} - \mathbf{x} \|^2}{2k^2} \right) \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def lwlr(testPoint, xArr, yArr, k=1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(ones((m,1)))
    for j in range(m):
        diffMat = testPoint - xMat[j,:] # 向量差(1, m)
        weights[j] = exp(diffMat*diffMat.T/(-2.0*k**2)) # 高斯核函数
    xTx = xMat.T * (multiply(weights,xMat))
    if linalg.det(xTx) == 0.0:
        print("Matrix is singular!")
        return
    ws = xTx.I * (xMat.T * (multiply(weights, yMat)))
    return testPoint * ws

def lwlrTest(testArr, xArr, yArr, k=1.0):
    m = shape(testArr)[0]
    yHat = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    return yHat
1
2
# 测试一个点的预测结果和真实结果对比
print(lwlr(xArr[0], xArr, yArr, 1.0),yArr[0])
[[ 3.12204471]] 3.176513
1
yHat = lwlrTest(xArr, xArr, yArr, 0.003)
1
2
3
4
5
6
7
8
9
10
# 绘制预测值和真实值对比图
xMat = mat(xArr)
srtInd = xMat[:, 1].argsort(0) # 输出排序后的索引
xSort = xMat[srtInd][:, 0, :] # 
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(xSort[:,1], yHat[srtInd])
ax.scatter(xMat[:,1].flatten().A[0], mat(yArr).T.flatten().A[0], s=2, c='red')
plt.show()
png

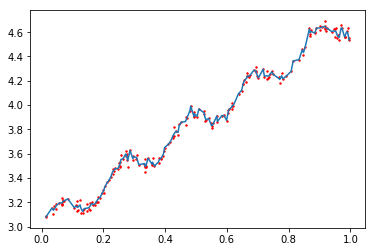
png

岭回归

当样本数量少于特征数量时，矩阵\(\mathbf{X}\)不满秩，为了解决这个问题，引入岭回归(ridge regression)。此时，回归系数的计算公式变为： \[ \mathbf{w}^* = (\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I})^{-1} \mathbf{X}^T \mathbf{y} \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def ridgeRegres(xMat, yMat, lam=0.2):
    """
    正则化的线性回归算法
    xArr: (m, n)
    yArr: (1, m)
    输出ws: (n, 1)
    """
    xTx = xMat.T*xMat + eye(shape(xMat)[1])*lam
    if linalg.det(xTx) == 0.0:
        print("Matrix is singular")
        return
    ws = xTx.I * (xMat.T*yMat)
    return ws

def ridgeTest(xArr, yArr):
    """
    对数据预处理，并测试不同alpha返回的权系数
    xArr: (m, n)
    yArr: (1, m)
    返回 wMat: (m, n)
    """
    xMat = mat(xArr); yMat = mat(yArr).T
    
    # 数据预处理
    yMean = mean(yMat, 0)
    yMat = yMat - yMean
    xMeans = mean(xMat, 0)
    xVar = var(xMat, 0)
    xMat = (xMat - xMeans)/xVar
    
    # 测试30次，每次使用不同的alpha作正则化因子
    numTestPts = 30
    wMat = zeros((numTestPts,shape(xMat)[1])) # (m, n)
    for i in range(numTestPts):
        ws = ridgeRegres(xMat, yMat, exp(i-10)) # n
        wMat[i,:] = ws.T
    return wMat
1
2
3
4
5
6
7
8
abX, abY = loadDataSet('abalone.txt')
rideWeights = ridgeTest(abX, abY)

import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(rideWeights)
plt.show()
png

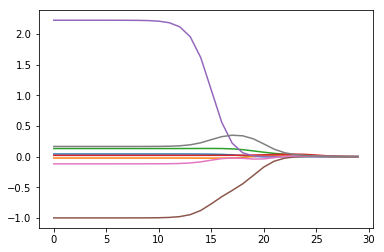
png

可以看出，权系数反应了哪些特征的影响最大，而随着\(\lambda\)的增大，权系数逐渐都缩小到0。一般在中间位置的效果最佳。

Lasso回归

实际上，岭回归和阻尼最小二乘法等价，阻尼最小二乘所增加的约束条件是： \[ \sum_{i=1}^{n} w_k^2 \leq \lambda \] 与岭回归类似，Lasso对回归系数增加如下约束： \[ \sum_{i=1}^{n} |w_k| \leq \lambda \] 该约束会使得回归系数分布更加稀疏。直接求解系数需要二次规划算法，比较费时，这里介绍一种贪心算法，叫做向前逐步回归。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def regularize(xMat):
    """
    xMat: (m, n)
    沿着列方向归一化处理
    """
    inMat = xMat.copy()
    inMeans = mean(inMat,0)   #
    inVar = var(inMat,0)      #
    inMat = (inMat - inMeans)/inVar
    return inMat

def rssError(yArr,yHatArr): 
    """
    计算均方误差
    """
    return ((yArr-yHatArr)**2).sum()

def stageWise(xArr,yArr,eps=0.01,numIt=100):
    """
    xArr: (m, n)
    yArr: (1, m)
    eps: 调整步长
    numIt: 迭代次数
    """
    xMat = mat(xArr); yMat = mat(yArr).T
    yMean = mean(yMat, 0)
    yMat = yMat - yMean
    xMat = regularize(xMat) # 按照均值为0，方差为1进行标准化处理
    m, n = shape(xMat)
    returnMat = zeros((numIt, n))
    ws = zeros((n, 1)); wsTest = ws.copy(); wsMax = ws.copy()
    
    for i in range(numIt):
        #print(ws.T)
        lowestError = inf
        
        # 对特征循环
        for j in range(n):
            for sign in [-1, 1]:
                wsTest = ws.copy()
                wsTest[j] += eps*sign # 调整权系数
                yTest = xMat*wsTest # 计算预测值
                rssE = rssError(yMat.A, yTest.A) # 计算预测误差
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        returnMat[i, :] = ws.T
    return returnMat
1
2
3
4
5
6
xArr, yArr = loadDataSet('abalone.txt')
stageWeights = stageWise(xArr, yArr, 0.001, 1000)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(stageWeights)
plt.show()
png

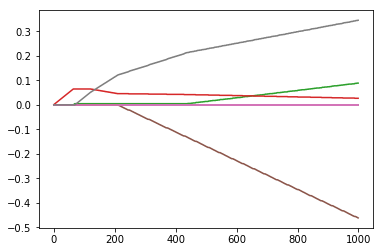
png

逐步线性回归的好处在于，可以快速的找到重要的特征，从而有可能及时停止对那些不重要特征的收集。

实例：预测乐高玩具价格

1
2


结论及讨论

结论

  • 优点：结果易于理解，计算不复杂
  • 缺点：对非线性拟合不好

讨论

  1. 对非线性回归问题，除局部加权线性回归外，还有一种简单有效的做法是引入高阶特征，然后用相同的程序进行线性回归。
  2. 线性回归是一种最重要、是最为常用的算法，同时也是神经网络方法的基础。神经网络通过加入层数来增加模型的泛化能力。

参考资料

  1. Peter Harrington, Machine learning in action, Manning Publications, 2012
  2. 周志华，机器学习，清华大学出版社， 2016