神经网络机器翻译机

发表于 | 分类于

本文将介绍注意力机制的基本原理，并通过Keras搭建一个神经网络机器翻译机以介绍注意力机制的实现过程，最后将其应用于日期格式翻译：从人类可读的日期（比如25th of June, 2009）翻译成机器可读的日期（2009-06-25）。该模型同样可以作为人类语言翻译的雏形。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from keras.layers import Bidirectional, Concatenate, Permute, Dot, Input, LSTM, Multiply
from keras.layers import RepeatVector, Dense, Activation, Lambda
from keras.optimizers import Adam
from keras.utils import to_categorical
from keras.models import load_model, Model
import keras.backend as K
import numpy as np

from faker import Faker
import random
from tqdm import tqdm
from babel.dates import format_date
from nmt_utils import *
import matplotlib.pyplot as plt
%matplotlib inline

将人类可读的日期翻译为机器可读的日期

这里你所建立的模型也可以用来将一种语言翻译成另一种余元，比如将英语翻译成印第安语。但是，语言翻译需要大量的数据集，往往需要在多个GPU上训练好几天。为了不适用海量数据集就可以测试这些模型，我们选择更加简单的“日期翻译”任务。

这个网络将写成不同形式的日期（比如"the 29th of August 1958", "03/30/1968", "24 JUNE 1987"）翻译成标准的机器可读的日期（比如"1958-08-29", "1968-03-30", "1987-06-24"）。我们训练这个网络使得它学会输出机器可读的形式：YYYY-MM-DD。

数据集

我们在10000个人类可读的日期和对应的标准化机器可读的日期作为数据集。下面加载数据集，并显示几个例子。

1
2
m = 10000
dataset, human_vocab, machine_vocab, inv_machine_vocab = load_dataset(m)
100%|██████████| 10000/10000 [00:01<00:00, 8664.72it/s]
1
dataset[:10]
[('9 may 1998', '1998-05-09'),
 ('10.09.70', '1970-09-10'),
 ('4/28/90', '1990-04-28'),
 ('thursday january 26 1995', '1995-01-26'),
 ('monday march 7 1983', '1983-03-07'),
 ('sunday may 22 1988', '1988-05-22'),
 ('tuesday july 8 2008', '2008-07-08'),
 ('08 sep 1999', '1999-09-08'),
 ('1 jan 1981', '1981-01-01'),
 ('monday may 22 1995', '1995-05-22')]

上面的命令下载了如下数据：

  • dataset: 一系列元组(人类可读日期，机器可读日期)
  • human_vocab: 人类可读日期中所使用的所有字符映射为整型索引的python字典
  • machine_vocab: 机器可读日期中所使用的所有字符映射为整型索引的python字典
  • inv_machine_vocab: machine_vocab的逆过程，从索引映射回字符

下面对数据进行预处理，并将纯文本数据映射到索引值。令Tx=30（假定人类可读的最大长度，如果更长，可以截断这个文本个），Ty=10（因为YYYY-MM-DD长度为10）。

1
2
3
4
5
6
7
8
Tx = 30
Ty = 10
X, Y, Xoh, Yoh = preprocess_data(dataset, human_vocab, machine_vocab, Tx, Ty)

print("X.shape:", X.shape)
print("Y.shape:", Y.shape)
print("Xoh.shape:", Xoh.shape)
print("Yoh.shape:", Yoh.shape)
X.shape: (10000, 30)
Y.shape: (10000, 10)
Xoh.shape: (10000, 30, 37)
Yoh.shape: (10000, 10, 11)

现在你有：

  • X: 训练集中预处理之后的人类可读日期，其中每个字符都通过human_vocab映射到对应的索引值。每个日期进一步用特殊字符（< pad >）补到Tx长。X.shape=(m,Tx)。
  • Y: 训练集中预处理之后的机器可读日期，其中每个字符都通过machine_vocab映射到对应的索引值。Y.shape=(m,Ty)。
  • Xoh: X的one-hot版本，采用human_vocab可以将元素为1的索引映射到对应的字符。Xoh.shape=(m, Tx, len(human_vocab))。
  • Yoh: Y的one-hot版本，采用machine_vocab可以将元素为1的索引映射到对应的字符。Yoh.shape=(m, Tx, len(machine_vocab))。其中machine_vocab=11。

下面查看预处理之后的训练样本。

1
2
3
4
5
6
7
8
9
index = 0
print("Source date:", dataset[index][0])
print("Target date:", dataset[index][1])
print()
print("Source after preprocessing (indices):", X[index])
print("Target after preprocessing (indices):", Y[index])
print()
print("Source after preprocessing (one-hot):", Xoh[index])
print("Target after preprocessing (one-hot):", Yoh[index])
Source date: 9 may 1998
Target date: 1998-05-09

Source after preprocessing (indices): [12  0 24 13 34  0  4 12 12 11 36 36 36 36 36 36 36 36 36 36 36 36 36 36 36
 36 36 36 36 36]
Target after preprocessing (indices): [ 2 10 10  9  0  1  6  0  1 10]

Source after preprocessing (one-hot): [[ 0.  0.  0. ...,  0.  0.  0.]
 [ 1.  0.  0. ...,  0.  0.  0.]
 [ 0.  0.  0. ...,  0.  0.  0.]
 ..., 
 [ 0.  0.  0. ...,  0.  0.  1.]
 [ 0.  0.  0. ...,  0.  0.  1.]
 [ 0.  0.  0. ...,  0.  0.  1.]]
Target after preprocessing (one-hot): [[ 0.  0.  1.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  1.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  1.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0.  1.  0.]
 [ 1.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  1.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  1.  0.  0.  0.  0.]
 [ 1.  0.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  1.  0.  0.  0.  0.  0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.  0.  0.  0.  0.  0.  1.]]

基于注意力机制的神经网络机器翻译系统

当你在将一段话从法语翻译成英语的过程中，你不会读完整段话，然后关上书本开始翻译。就算在翻译的过程中，你也是读了又读，然后聚焦在你要写下翻译对应的那部分法语部分。

注意力机制告诉神经网络翻译系统：每一步需要注意的部分

注意力机制

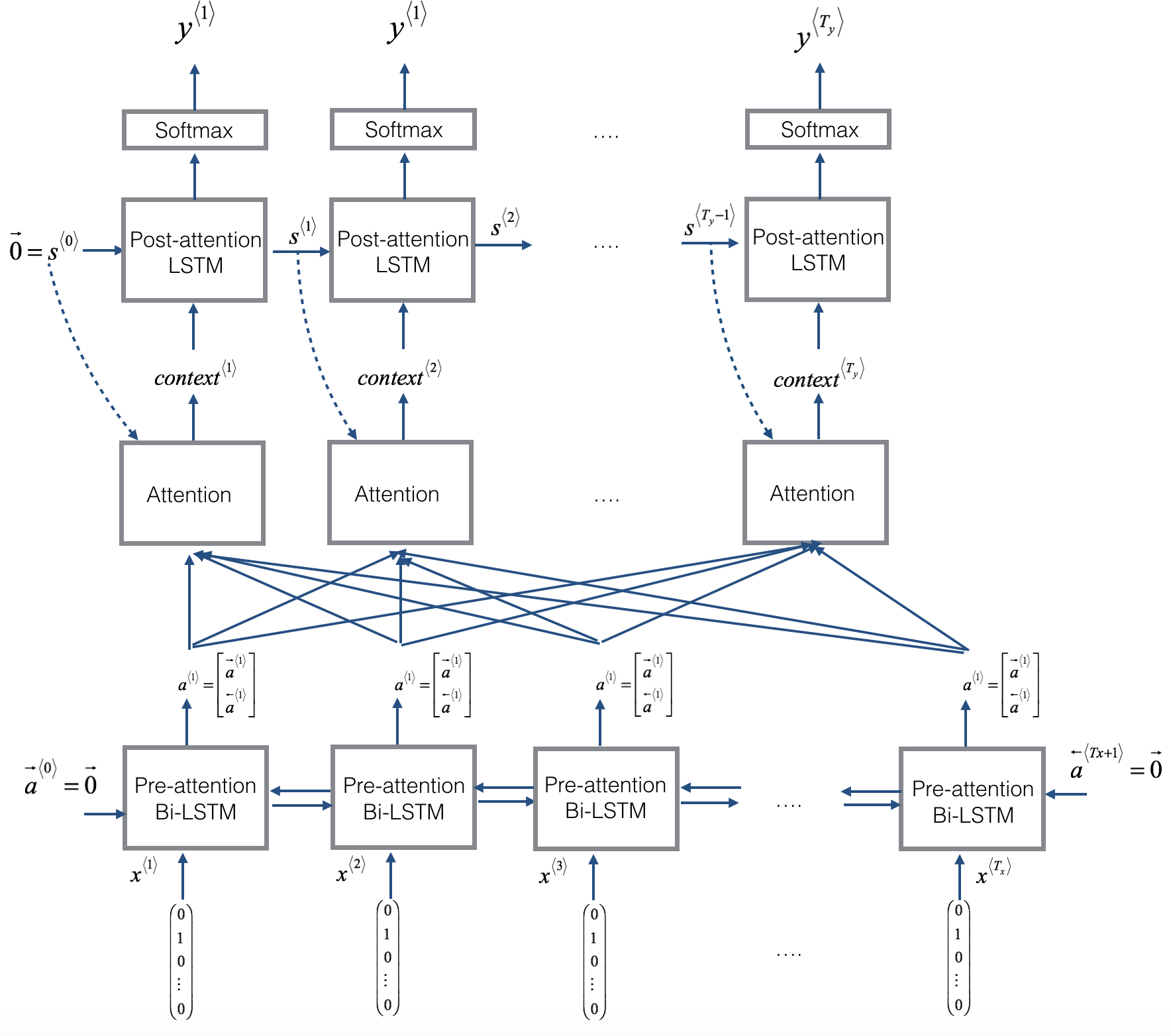
这部分将实现注意力机制。下图显示了这种机制的工作原理。
图 1: 基于注意力机制的神经网络机器翻译系统。左图是完整模型；右图是注意力模块

该模型具有以下特性：

  • 左图的模型中有两个独立的LSTMs。下方的LSTM是双向的，且在注意力机制的前面，被称之为预注意力双向LSTM。上方的LSTM在注意力机制之后，被称为后注意力LSTM。预注意力双向LSTM通过\(T_x\)个时间步，后注意力LSTM通过\(T_y\)个时间步
  • 后注意力LSTM将\(s^{<t>},c^{<t>}\)从一个时间步传到下一个时间步。但是，和语言生成模型不同的是后注意力LSTM在\(t\)时刻，并没有将之前生成的输出\(y^{<t-1>}\)作为输入。原因是在这个例子中，YYYY-MM-DD日期不像语言模型那样，相邻之间的字符串高度相关。
  • 我们采用\(a^{\langle t \rangle} = [\overrightarrow{a}^{\langle t \rangle}; \overleftarrow{a}^{\langle t \rangle}]\)代表将预训练双向LSTM的正向和反向激励合并。
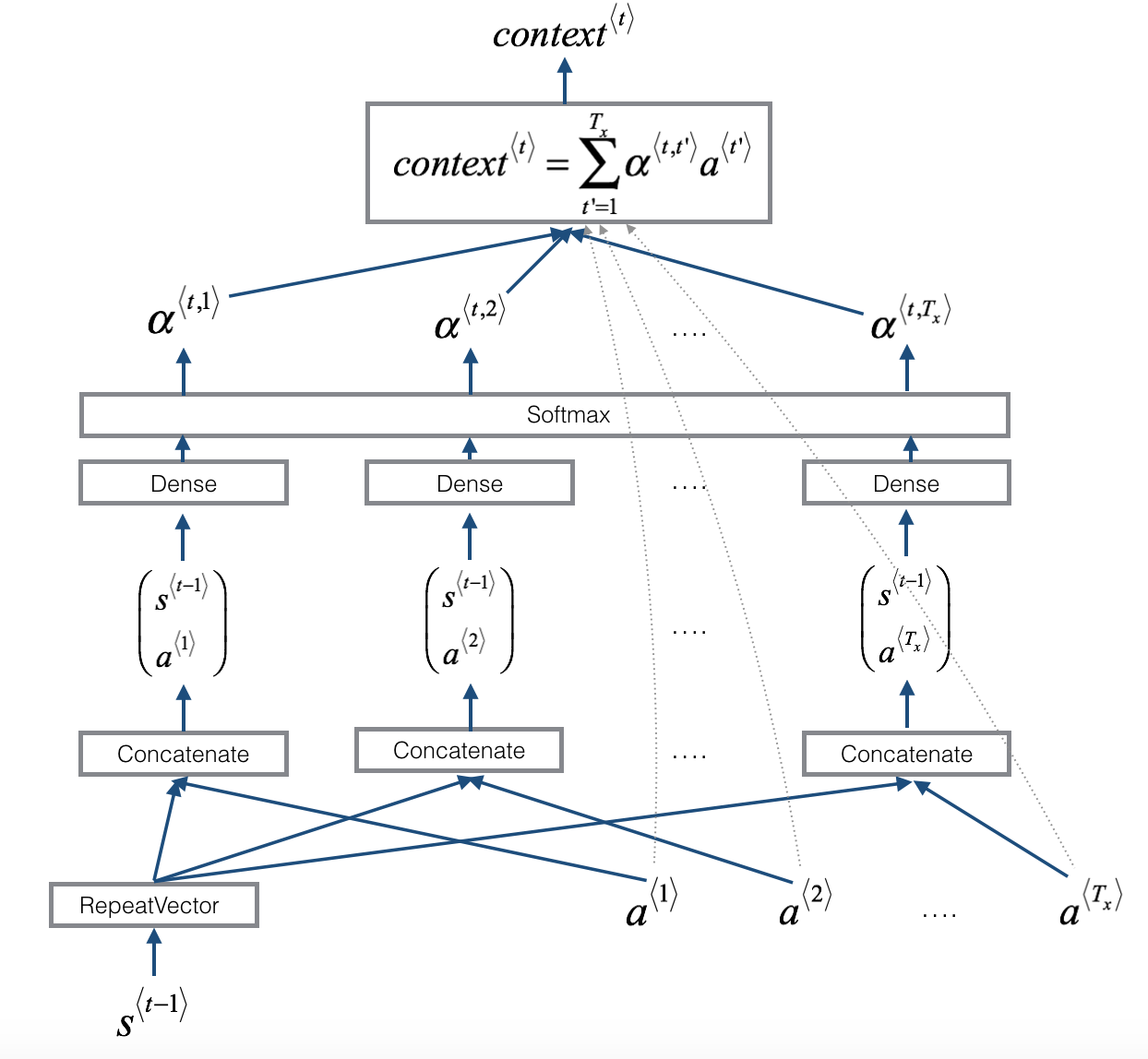
  • 右图使用RepeatVector节点将\(s^{\langle t-1 \rangle}\)的值拷贝了\(T_x\)次，然后用Concatenation合并\(s^{\langle t-1 \rangle}\)和\(a^{\langle t \rangle}\)，计算\(e^{\langle t, t'}\)。然后传到softmax层计算\(\alpha^{\langle t, t' \rangle}\)。下面会使用Keras详细介绍如何使用RepeatVector和Concatenation。

1) one_step_attention(): 在时间\(t\)，给定双向LSTM的所有隐藏层状态（\([a^{<1>},a^{<2>}, ..., a^{<T_x>}]\)）和第二个LSTM层的隐藏状态(\(s^{<t-1>}\))，one_step_attention()将计算注意力函数(\([\alpha^{<t,1>},\alpha^{<t,2>}, ..., \alpha^{<t,T_x>}]\))和输出文本向量（如图右所示），\[context^{<t>} = \sum_{t' = 0}^{T_x} \alpha^{<t,t'>}a^{<t'>}\tag{1}\]。

注意：这里使用\(context^{\langle t \rangle}\)表示文本向量，而\(c^{\langle t \rangle}\)用来表示LSTM的内部记忆单元变量。

2) model(): 实现整个模型。首先运行双向LSTM得到\([a^{<1>},a^{<2>}, ..., a^{<T_x>}]\)。然后调用one_step_attention() \(T_y\) 次。每次计算内容向量\(c^{<t>}\)。将内容向量输入到第二个LSTM，经过带softmax激活函数的全连接层，得到预测值\(\hat{y}^{<t>}\)

注意：函数model()调用one_step_attention()\(T_y\)次，每次共享权函数。在Keras中实现共享权函数的层：
1. 定义层对象（比如作为全局变量）
2. 正传输入时调用这些对象

下面是需要用到的一些Keras函数以及帮助文档：
RepeatVector(), Concatenate(), Dense(), Activation(), Dot().

1
2
3
4
5
6
# Defined shared layers as global variables
repeator = RepeatVector(Tx)
concatenator = Concatenate(axis=-1)
densor = Dense(1, activation = "relu")
activator = Activation(softmax, name='attention_weights') # We are using a custom softmax(axis = 1) loaded in this notebook
dotor = Dot(axes = 1)

使用上面提供的函数实现函数one_step_attention()。为了在其中一层正传一个Keras向量X，使用layer(X) (或在多个输入的情况下 layer([X,Y]))。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# GRADED FUNCTION: one_step_attention

def one_step_attention(a, s_prev):
    """
    Performs one step of attention: Outputs a context vector computed as a dot product of the attention weights
    "alphas" and the hidden states "a" of the Bi-LSTM.
    
    Arguments:
    a -- hidden state output of the Bi-LSTM, numpy-array of shape (m, Tx, 2*n_a)
    s_prev -- previous hidden state of the (post-attention) LSTM, numpy-array of shape (m, n_s)
    
    Returns:
    context -- context vector, input of the next (post-attetion) LSTM cell
    """
    
    ### START CODE HERE ###
    # Use repeator to repeat s_prev to be of shape (m, Tx, n_s) so that you can concatenate it with all hidden states "a" (≈ 1 line)
    s_prev = repeator(s_prev)
    # Use concatenator to concatenate a and s_prev on the last axis (≈ 1 line)
    concat = concatenator([a, s_prev])
    # Use densor to propagate concat through a small fully-connected neural network to compute the "energies" variable e. (≈1 lines)
    e = densor(concat)
    # Use activator and e to compute the attention weights "alphas" (≈ 1 line)
    alphas = activator(e)
    # Use dotor together with "alphas" and "a" to compute the context vector to be given to the next (post-attention) LSTM-cell (≈ 1 line)
    context = dotor([alphas, a])
    ### END CODE HERE ###
    
    return context

下面实现函数model()，定义全局层以实现权值共享

1
2
3
4
n_a = 64
n_s = 128
post_activation_LSTM_cell = LSTM(n_s, return_state = True)
output_layer = Dense(len(machine_vocab), activation=softmax)

下面调用这些层\(T_x\)次，生成输出，其中参数不会重新初始化。下面是详细步骤：

  1. 在双向LSTM中正传输入Bidirectional LSTM
  2. 循环\(t = 0, \dots, T_y-1\):
    1. 对 \([\alpha^{<t,1>},\alpha^{<t,2>}, ..., \alpha^{<t,T_x>}]\) 和 \(s^{<t-1>}\) 调用 one_step_attention()获得内容向量\(context^{<t>}\) .
    2. 给定 \(context^{<t>}\)，输入到后注意力LSTM单元. 输入的是这个神经元的前一个隐藏状态 \(s^{\langle t-1\rangle}\) 和 单元状态\(c^{\langle t-1\rangle}\)，输入组合成initial_state= [previous hidden state, previous cell state]. 返回新的隐藏状态 \(s^{<t>}\) 和新的神经元状态 \(c^{<t>}\).
    3. 对\(s^{<t>}\)应用softmax层, 得到输出.
    4. 将输出添加到输出列表，保存输出.
  3. 创建Keras模型实例，包含三个输入 ("输入", \(s^{<0>}\) 和 \(c^{<0>}\)) 和 输出一系列 "outputs".
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
# GRADED FUNCTION: model

def model(Tx, Ty, n_a, n_s, human_vocab_size, machine_vocab_size):
    """
    Arguments:
    Tx -- length of the input sequence
    Ty -- length of the output sequence
    n_a -- hidden state size of the Bi-LSTM
    n_s -- hidden state size of the post-attention LSTM
    human_vocab_size -- size of the python dictionary "human_vocab"
    machine_vocab_size -- size of the python dictionary "machine_vocab"

    Returns:
    model -- Keras model instance
    """
    
    # Define the inputs of your model with a shape (Tx,)
    # Define s0 and c0, initial hidden state for the decoder LSTM of shape (n_s,)
    X = Input(shape=(Tx, human_vocab_size))
    s0 = Input(shape=(n_s,), name='s0')
    c0 = Input(shape=(n_s,), name='c0')
    s = s0
    c = c0
    
    # Initialize empty list of outputs
    outputs = []
    
    ### START CODE HERE ###
    
    # Step 1: Define your pre-attention Bi-LSTM. Remember to use return_sequences=True. (≈ 1 line)
    a = Bidirectional(LSTM(n_a, return_sequences=True))(X)
    
    # Step 2: Iterate for Ty steps
    for t in range(Ty):
    
        # Step 2.A: Perform one step of the attention mechanism to get back the context vector at step t (≈ 1 line)
        context = one_step_attention(a, s)
        
        # Step 2.B: Apply the post-attention LSTM cell to the "context" vector.
        # Don't forget to pass: initial_state = [hidden state, cell state] (≈ 1 line)
        s, _, c = post_activation_LSTM_cell(context, initial_state=[s, c])
        
        # Step 2.C: Apply Dense layer to the hidden state output of the post-attention LSTM (≈ 1 line)
        out = output_layer(s)
        
        # Step 2.D: Append "out" to the "outputs" list (≈ 1 line)
        outputs.append(out)
    
    # Step 3: Create model instance taking three inputs and returning the list of outputs. (≈ 1 line)
    model = Model([X, s0, c0], outputs)
    
    ### END CODE HERE ###
    
    return model

创建模型

1
model = model(Tx, Ty, n_a, n_s, len(human_vocab), len(machine_vocab))
WARNING:tensorflow:From /home/seisinv/anaconda3/envs/fwi_ai/lib/python3.5/site-packages/keras/backend/tensorflow_backend.py:1190: calling reduce_sum (from tensorflow.python.ops.math_ops) with keep_dims is deprecated and will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead
WARNING:tensorflow:From /home/seisinv/anaconda3/envs/fwi_ai/lib/python3.5/site-packages/keras/backend/tensorflow_backend.py:1154: calling reduce_max (from tensorflow.python.ops.math_ops) with keep_dims is deprecated and will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead
1
model.summary()
____________________________________________________________________________________________________
Layer (type)                     Output Shape          Param #     Connected to                     
====================================================================================================
input_1 (InputLayer)             (None, 30, 37)        0                                            
____________________________________________________________________________________________________
s0 (InputLayer)                  (None, 128)           0                                            
____________________________________________________________________________________________________
bidirectional_1 (Bidirectional)  (None, 30, 128)       52224       input_1[0][0]                    
____________________________________________________________________________________________________
repeat_vector_1 (RepeatVector)   (None, 30, 128)       0           s0[0][0]                         
                                                                   lstm_1[0][0]                     
                                                                   lstm_1[1][0]                     
                                                                   lstm_1[2][0]                     
                                                                   lstm_1[3][0]                     
                                                                   lstm_1[4][0]                     
                                                                   lstm_1[5][0]                     
                                                                   lstm_1[6][0]                     
                                                                   lstm_1[7][0]                     
                                                                   lstm_1[8][0]                     
____________________________________________________________________________________________________
concatenate_1 (Concatenate)      (None, 30, 256)       0           bidirectional_1[0][0]            
                                                                   repeat_vector_1[0][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[1][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[2][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[3][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[4][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[5][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[6][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[7][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[8][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[9][0]            
____________________________________________________________________________________________________
dense_1 (Dense)                  (None, 30, 1)         257         concatenate_1[0][0]              
                                                                   concatenate_1[1][0]              
                                                                   concatenate_1[2][0]              
                                                                   concatenate_1[3][0]              
                                                                   concatenate_1[4][0]              
                                                                   concatenate_1[5][0]              
                                                                   concatenate_1[6][0]              
                                                                   concatenate_1[7][0]              
                                                                   concatenate_1[8][0]              
                                                                   concatenate_1[9][0]              
____________________________________________________________________________________________________
attention_weights (Activation)   (None, 30, 1)         0           dense_1[0][0]                    
                                                                   dense_1[1][0]                    
                                                                   dense_1[2][0]                    
                                                                   dense_1[3][0]                    
                                                                   dense_1[4][0]                    
                                                                   dense_1[5][0]                    
                                                                   dense_1[6][0]                    
                                                                   dense_1[7][0]                    
                                                                   dense_1[8][0]                    
                                                                   dense_1[9][0]                    
____________________________________________________________________________________________________
dot_1 (Dot)                      (None, 1, 128)        0           attention_weights[0][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[1][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[2][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[3][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[4][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[5][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[6][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[7][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[8][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[9][0]          
                                                                   bidirectional_1[0][0]            
____________________________________________________________________________________________________
c0 (InputLayer)                  (None, 128)           0                                            
____________________________________________________________________________________________________
lstm_1 (LSTM)                    [(None, 128), (None,  131584      dot_1[0][0]                      
                                                                   s0[0][0]                         
                                                                   c0[0][0]                         
                                                                   dot_1[1][0]                      
                                                                   lstm_1[0][0]                     
                                                                   lstm_1[0][2]                     
                                                                   dot_1[2][0]                      
                                                                   lstm_1[1][0]                     
                                                                   lstm_1[1][2]                     
                                                                   dot_1[3][0]                      
                                                                   lstm_1[2][0]                     
                                                                   lstm_1[2][2]                     
                                                                   dot_1[4][0]                      
                                                                   lstm_1[3][0]                     
                                                                   lstm_1[3][2]                     
                                                                   dot_1[5][0]                      
                                                                   lstm_1[4][0]                     
                                                                   lstm_1[4][2]                     
                                                                   dot_1[6][0]                      
                                                                   lstm_1[5][0]                     
                                                                   lstm_1[5][2]                     
                                                                   dot_1[7][0]                      
                                                                   lstm_1[6][0]                     
                                                                   lstm_1[6][2]                     
                                                                   dot_1[8][0]                      
                                                                   lstm_1[7][0]                     
                                                                   lstm_1[7][2]                     
                                                                   dot_1[9][0]                      
                                                                   lstm_1[8][0]                     
                                                                   lstm_1[8][2]                     
____________________________________________________________________________________________________
dense_2 (Dense)                  (None, 11)            1419        lstm_1[0][0]                     
                                                                   lstm_1[1][0]                     
                                                                   lstm_1[2][0]                     
                                                                   lstm_1[3][0]                     
                                                                   lstm_1[4][0]                     
                                                                   lstm_1[5][0]                     
                                                                   lstm_1[6][0]                     
                                                                   lstm_1[7][0]                     
                                                                   lstm_1[8][0]                     
                                                                   lstm_1[9][0]                     
====================================================================================================
Total params: 185,484
Trainable params: 185,484
Non-trainable params: 0
____________________________________________________________________________________________________

预计的输出:

<tr>
    <td>
        **Total params:**
    </td>
    <td>
     185,484
    </td>
</tr>
    <tr>
    <td>
        **Trainable params:**
    </td>
    <td>
     185,484
    </td>
</tr>
        <tr>
    <td>
        **Non-trainable params:**
    </td>
    <td>
     0
    </td>
</tr>
                <tr>
    <td>
        **bidirectional_1's output shape **
    </td>
    <td>
     (None, 30, 128)  
    </td>
</tr>
<tr>
    <td>
        **repeat_vector_1's output shape **
    </td>
    <td>
     (None, 30, 128)  
    </td>
</tr>
            <tr>
    <td>
        **concatenate_1's output shape **
    </td>
    <td>
     (None, 30, 256) 
    </td>
</tr>
        <tr>
    <td>
        **attention_weights's output shape **
    </td>
    <td>
     (None, 30, 1)  
    </td>
</tr>
    <tr>
    <td>
        **dot_1's output shape **
    </td>
    <td>
     (None, 1, 128) 
    </td>
</tr>
       <tr>
    <td>
        **dense_2's output shape **
    </td>
    <td>
     (None, 11) 
    </td>
</tr>

和之前一样，在Keras中创建好模型之后，需要编译并定义损失函数，优化器以及要使用的性能度量。使用categorical_crossentropy损失函数，自定义的优化器optimizer (learning rate = 0.005, \(\beta_1 = 0.9\), \(\beta_2 = 0.999\), decay = 0.01)和['accuracy']作为性能度量

1
2
3
4
### START CODE HERE ### (≈2 lines)
opt = Adam(lr = 0.005, beta_1=0.9, beta_2=0.999, decay = 0.01)
model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
### END CODE HERE ###
WARNING:tensorflow:From /home/seisinv/anaconda3/envs/fwi_ai/lib/python3.5/site-packages/keras/backend/tensorflow_backend.py:1297: calling reduce_mean (from tensorflow.python.ops.math_ops) with keep_dims is deprecated and will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead

最后一步：定义所有的输入和输出，并拟合模型。

  • X的维度为\((m = 10000, T_x = 30)\) 包含所有的训练样本.
  • 创建 s0 和 c0 初始化 post_activation_LSTM_cell 为0.
  • 给定model() , 输出 "outputs" 为 含11 个元素的序列，维度为 (m, T_y). 因此: outputs[i][0], ..., outputs[i][Ty] 第\(i\) 个样本 (X[i])的真实标签（字符）(X[i]). 更一般的, outputs[i][j] 为第\(i^{th}\)个训练样本第\(j^{th}\)个字符的真实标签。
1
2
3
s0 = np.zeros((m, n_s))
c0 = np.zeros((m, n_s))
outputs = list(Yoh.swapaxes(0,1))

下面拟合模型，只执行一次迭代。

1
model.fit([Xoh, s0, c0], outputs, epochs=10, batch_size=100)
Epoch 1/10
10000/10000 [==============================] - 33s - loss: 7.4147 - dense_2_loss_1: 0.1020 - dense_2_loss_2: 0.0813 - dense_2_loss_3: 0.6302 - dense_2_loss_4: 1.8963 - dense_2_loss_5: 0.0076 - dense_2_loss_6: 0.1562 - dense_2_loss_7: 1.6076 - dense_2_loss_8: 0.0046 - dense_2_loss_9: 0.9532 - dense_2_loss_10: 1.9758 - dense_2_acc_1: 0.9687 - dense_2_acc_2: 0.9723 - dense_2_acc_3: 0.7522 - dense_2_acc_4: 0.3075 - dense_2_acc_5: 0.9999 - dense_2_acc_6: 0.9523 - dense_2_acc_7: 0.4073 - dense_2_acc_8: 1.0000 - dense_2_acc_9: 0.5871 - dense_2_acc_10: 0.2662    
Epoch 2/10
10000/10000 [==============================] - 33s - loss: 5.3461 - dense_2_loss_1: 0.0713 - dense_2_loss_2: 0.0602 - dense_2_loss_3: 0.4529 - dense_2_loss_4: 1.2917 - dense_2_loss_5: 0.0059 - dense_2_loss_6: 0.1070 - dense_2_loss_7: 1.2188 - dense_2_loss_8: 0.0054 - dense_2_loss_9: 0.7383 - dense_2_loss_10: 1.3946 - dense_2_acc_1: 0.9774 - dense_2_acc_2: 0.9792 - dense_2_acc_3: 0.8190 - dense_2_acc_4: 0.5389 - dense_2_acc_5: 0.9999 - dense_2_acc_6: 0.9695 - dense_2_acc_7: 0.5465 - dense_2_acc_8: 0.9998 - dense_2_acc_9: 0.6832 - dense_2_acc_10: 0.4885    
Epoch 3/10
10000/10000 [==============================] - 33s - loss: 3.7412 - dense_2_loss_1: 0.0584 - dense_2_loss_2: 0.0498 - dense_2_loss_3: 0.3604 - dense_2_loss_4: 0.8144 - dense_2_loss_5: 0.0049 - dense_2_loss_6: 0.0930 - dense_2_loss_7: 0.9398 - dense_2_loss_8: 0.0045 - dense_2_loss_9: 0.5976 - dense_2_loss_10: 0.8183 - dense_2_acc_1: 0.9810 - dense_2_acc_2: 0.9819 - dense_2_acc_3: 0.8534 - dense_2_acc_4: 0.7320 - dense_2_acc_5: 1.0000 - dense_2_acc_6: 0.9734 - dense_2_acc_7: 0.6660 - dense_2_acc_8: 1.0000 - dense_2_acc_9: 0.7660 - dense_2_acc_10: 0.7118    
Epoch 4/10
10000/10000 [==============================] - 33s - loss: 2.6837 - dense_2_loss_1: 0.0485 - dense_2_loss_2: 0.0414 - dense_2_loss_3: 0.2905 - dense_2_loss_4: 0.5242 - dense_2_loss_5: 0.0043 - dense_2_loss_6: 0.0762 - dense_2_loss_7: 0.6770 - dense_2_loss_8: 0.0042 - dense_2_loss_9: 0.4856 - dense_2_loss_10: 0.5319 - dense_2_acc_1: 0.9843 - dense_2_acc_2: 0.9844 - dense_2_acc_3: 0.8810 - dense_2_acc_4: 0.8535 - dense_2_acc_5: 1.0000 - dense_2_acc_6: 0.9779 - dense_2_acc_7: 0.7785 - dense_2_acc_8: 1.0000 - dense_2_acc_9: 0.8240 - dense_2_acc_10: 0.8149    
Epoch 5/10
10000/10000 [==============================] - 34s - loss: 2.0444 - dense_2_loss_1: 0.0419 - dense_2_loss_2: 0.0348 - dense_2_loss_3: 0.2438 - dense_2_loss_4: 0.3605 - dense_2_loss_5: 0.0035 - dense_2_loss_6: 0.0624 - dense_2_loss_7: 0.4857 - dense_2_loss_8: 0.0038 - dense_2_loss_9: 0.4024 - dense_2_loss_10: 0.4056 - dense_2_acc_1: 0.9866 - dense_2_acc_2: 0.9865 - dense_2_acc_3: 0.8946 - dense_2_acc_4: 0.8977 - dense_2_acc_5: 1.0000 - dense_2_acc_6: 0.9815 - dense_2_acc_7: 0.8585 - dense_2_acc_8: 0.9998 - dense_2_acc_9: 0.8549 - dense_2_acc_10: 0.8575    
Epoch 6/10
10000/10000 [==============================] - 34s - loss: 1.6617 - dense_2_loss_1: 0.0354 - dense_2_loss_2: 0.0283 - dense_2_loss_3: 0.2110 - dense_2_loss_4: 0.2748 - dense_2_loss_5: 0.0029 - dense_2_loss_6: 0.0569 - dense_2_loss_7: 0.3805 - dense_2_loss_8: 0.0030 - dense_2_loss_9: 0.3356 - dense_2_loss_10: 0.3333 - dense_2_acc_1: 0.9878 - dense_2_acc_2: 0.9891 - dense_2_acc_3: 0.9083 - dense_2_acc_4: 0.9206 - dense_2_acc_5: 1.0000 - dense_2_acc_6: 0.9843 - dense_2_acc_7: 0.8917 - dense_2_acc_8: 1.0000 - dense_2_acc_9: 0.8778 - dense_2_acc_10: 0.8811    
Epoch 7/10
10000/10000 [==============================] - 34s - loss: 1.3926 - dense_2_loss_1: 0.0286 - dense_2_loss_2: 0.0225 - dense_2_loss_3: 0.1850 - dense_2_loss_4: 0.2215 - dense_2_loss_5: 0.0026 - dense_2_loss_6: 0.0493 - dense_2_loss_7: 0.3083 - dense_2_loss_8: 0.0026 - dense_2_loss_9: 0.2848 - dense_2_loss_10: 0.2876 - dense_2_acc_1: 0.9923 - dense_2_acc_2: 0.9916 - dense_2_acc_3: 0.9179 - dense_2_acc_4: 0.9288 - dense_2_acc_5: 1.0000 - dense_2_acc_6: 0.9848 - dense_2_acc_7: 0.9155 - dense_2_acc_8: 1.0000 - dense_2_acc_9: 0.8996 - dense_2_acc_10: 0.8946    
Epoch 8/10
10000/10000 [==============================] - 34s - loss: 1.2089 - dense_2_loss_1: 0.0258 - dense_2_loss_2: 0.0195 - dense_2_loss_3: 0.1666 - dense_2_loss_4: 0.1916 - dense_2_loss_5: 0.0021 - dense_2_loss_6: 0.0450 - dense_2_loss_7: 0.2664 - dense_2_loss_8: 0.0023 - dense_2_loss_9: 0.2382 - dense_2_loss_10: 0.2514 - dense_2_acc_1: 0.9920 - dense_2_acc_2: 0.9921 - dense_2_acc_3: 0.9293 - dense_2_acc_4: 0.9394 - dense_2_acc_5: 1.0000 - dense_2_acc_6: 0.9863 - dense_2_acc_7: 0.9297 - dense_2_acc_8: 1.0000 - dense_2_acc_9: 0.9187 - dense_2_acc_10: 0.9044    
Epoch 9/10
10000/10000 [==============================] - 34s - loss: 1.0653 - dense_2_loss_1: 0.0218 - dense_2_loss_2: 0.0162 - dense_2_loss_3: 0.1498 - dense_2_loss_4: 0.1703 - dense_2_loss_5: 0.0019 - dense_2_loss_6: 0.0412 - dense_2_loss_7: 0.2351 - dense_2_loss_8: 0.0021 - dense_2_loss_9: 0.2030 - dense_2_loss_10: 0.2238 - dense_2_acc_1: 0.9929 - dense_2_acc_2: 0.9939 - dense_2_acc_3: 0.9392 - dense_2_acc_4: 0.9448 - dense_2_acc_5: 1.0000 - dense_2_acc_6: 0.9865 - dense_2_acc_7: 0.9357 - dense_2_acc_8: 1.0000 - dense_2_acc_9: 0.9339 - dense_2_acc_10: 0.9164    
Epoch 10/10
10000/10000 [==============================] - 34s - loss: 0.9475 - dense_2_loss_1: 0.0194 - dense_2_loss_2: 0.0142 - dense_2_loss_3: 0.1359 - dense_2_loss_4: 0.1506 - dense_2_loss_5: 0.0018 - dense_2_loss_6: 0.0380 - dense_2_loss_7: 0.2107 - dense_2_loss_8: 0.0019 - dense_2_loss_9: 0.1732 - dense_2_loss_10: 0.2018 - dense_2_acc_1: 0.9939 - dense_2_acc_2: 0.9949 - dense_2_acc_3: 0.9481 - dense_2_acc_4: 0.9536 - dense_2_acc_5: 1.0000 - dense_2_acc_6: 0.9873 - dense_2_acc_7: 0.9427 - dense_2_acc_8: 1.0000 - dense_2_acc_9: 0.9458 - dense_2_acc_10: 0.9228    





<keras.callbacks.History at 0x7fc615040ef0>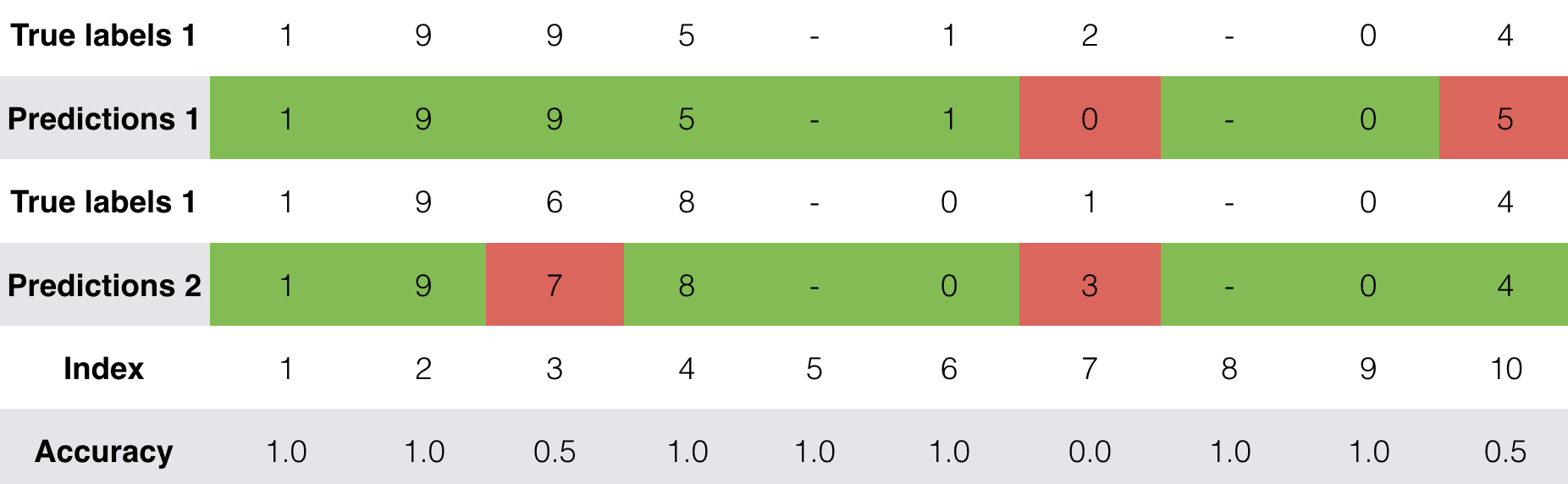
在训练过程中，输出的每10个位置你可以看到损失函数和精度信息。下表是当batch大小为2个样本时的精度。
Thus, dense_2_acc_8: 0.89 means that you are predicting the 7th character of the output correctly 89% of the time in the current batch of data.

下面是训练好的模型，你也可以增加迭代次数获得类似的模型。

1
#model.load_weights('models/model.h5')
1
2
3
4
5
6
7
8
9
10
11
EXAMPLES = ['3 May 1979', '5 April 09', '21th of August 2016', 'Tue 10 Jul 2007', 'Saturday May 9 2018', 'March 3 2001', 'March 3rd 2001', '1 March 2001']
for example in EXAMPLES:
    
    source = string_to_int(example, Tx, human_vocab)
    source = np.array(list(map(lambda x: to_categorical(x, num_classes=len(human_vocab)), source))).swapaxes(0,1)
    prediction = model.predict([source, s0, c0])
    prediction = np.argmax(prediction, axis = -1)
    output = [inv_machine_vocab[int(i)] for i in prediction]
    
    print("source:", example)
    print("output:", ''.join(output))
source: 3 May 1979
output: 1979-05-03
source: 5 April 09
output: 2009-04-05
source: 21th of August 2016
output: 2016-08-11
source: Tue 10 Jul 2007
output: 2007-07-10
source: Saturday May 9 2018
output: 2018-05-09
source: March 3 2001
output: 2011-03-03
source: March 3rd 2001
output: 2011-03-03
source: 1 March 2001
output: 2010-03-01

可视化注意力

由于这个问题有固定的输出长度\(T_y=10\)，因此也有可能采用常规的神经网络：用10个不同的softmax单元生成10个字符。但是注意力模型的一个优势是：输出的每个部分（比如月份）知道它仅仅依赖于输出的一小部分（比如输入中给定月份的字符）。我们可以可视化这个输出注意输入的哪个部分。

比如将"Saturday 9 May 2018" 翻译成 "2018-05-09"。如果可视化\(\alpha^{\langle t, t' \rangle}\)，将会得到：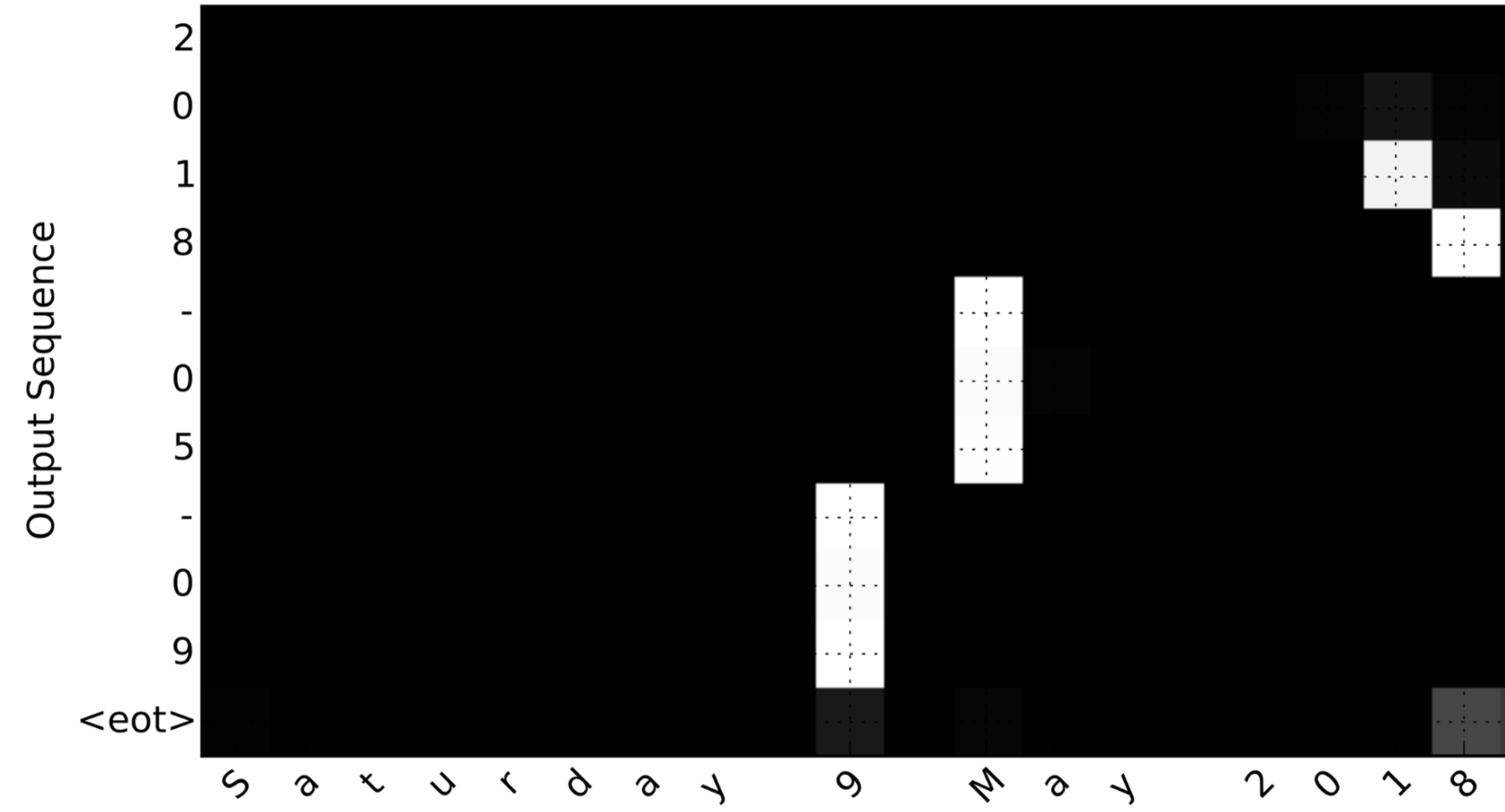
Figure 8: Full Attention Map

注意到：输出是如何忽略输入的"Saturday"部分的。没有另个一个输出时间步关注太多到那部分。我们也能看到每个输出关注它需要注意的部分，9被翻译成09，May被翻译成05。为了生成"2018"，需要关注输入的"18"部分。

获取网络的激励

为了可视化网络中注意力值，首先要正传一个样例，然后可视化\(\alpha^{\langle t, t' \rangle}\)的值。

为了找到注意力值的位置，打印模型的总结。

1
model.summary()
____________________________________________________________________________________________________
Layer (type)                     Output Shape          Param #     Connected to                     
====================================================================================================
input_1 (InputLayer)             (None, 30, 37)        0                                            
____________________________________________________________________________________________________
s0 (InputLayer)                  (None, 128)           0                                            
____________________________________________________________________________________________________
bidirectional_1 (Bidirectional)  (None, 30, 128)       52224       input_1[0][0]                    
____________________________________________________________________________________________________
repeat_vector_1 (RepeatVector)   (None, 30, 128)       0           s0[0][0]                         
                                                                   lstm_1[0][0]                     
                                                                   lstm_1[1][0]                     
                                                                   lstm_1[2][0]                     
                                                                   lstm_1[3][0]                     
                                                                   lstm_1[4][0]                     
                                                                   lstm_1[5][0]                     
                                                                   lstm_1[6][0]                     
                                                                   lstm_1[7][0]                     
                                                                   lstm_1[8][0]                     
____________________________________________________________________________________________________
concatenate_1 (Concatenate)      (None, 30, 256)       0           bidirectional_1[0][0]            
                                                                   repeat_vector_1[0][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[1][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[2][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[3][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[4][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[5][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[6][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[7][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[8][0]            
                                                                   bidirectional_1[0][0]            
                                                                   repeat_vector_1[9][0]            
____________________________________________________________________________________________________
dense_1 (Dense)                  (None, 30, 1)         257         concatenate_1[0][0]              
                                                                   concatenate_1[1][0]              
                                                                   concatenate_1[2][0]              
                                                                   concatenate_1[3][0]              
                                                                   concatenate_1[4][0]              
                                                                   concatenate_1[5][0]              
                                                                   concatenate_1[6][0]              
                                                                   concatenate_1[7][0]              
                                                                   concatenate_1[8][0]              
                                                                   concatenate_1[9][0]              
____________________________________________________________________________________________________
attention_weights (Activation)   (None, 30, 1)         0           dense_1[0][0]                    
                                                                   dense_1[1][0]                    
                                                                   dense_1[2][0]                    
                                                                   dense_1[3][0]                    
                                                                   dense_1[4][0]                    
                                                                   dense_1[5][0]                    
                                                                   dense_1[6][0]                    
                                                                   dense_1[7][0]                    
                                                                   dense_1[8][0]                    
                                                                   dense_1[9][0]                    
____________________________________________________________________________________________________
dot_1 (Dot)                      (None, 1, 128)        0           attention_weights[0][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[1][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[2][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[3][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[4][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[5][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[6][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[7][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[8][0]          
                                                                   bidirectional_1[0][0]            
                                                                   attention_weights[9][0]          
                                                                   bidirectional_1[0][0]            
____________________________________________________________________________________________________
c0 (InputLayer)                  (None, 128)           0                                            
____________________________________________________________________________________________________
lstm_1 (LSTM)                    [(None, 128), (None,  131584      dot_1[0][0]                      
                                                                   s0[0][0]                         
                                                                   c0[0][0]                         
                                                                   dot_1[1][0]                      
                                                                   lstm_1[0][0]                     
                                                                   lstm_1[0][2]                     
                                                                   dot_1[2][0]                      
                                                                   lstm_1[1][0]                     
                                                                   lstm_1[1][2]                     
                                                                   dot_1[3][0]                      
                                                                   lstm_1[2][0]                     
                                                                   lstm_1[2][2]                     
                                                                   dot_1[4][0]                      
                                                                   lstm_1[3][0]                     
                                                                   lstm_1[3][2]                     
                                                                   dot_1[5][0]                      
                                                                   lstm_1[4][0]                     
                                                                   lstm_1[4][2]                     
                                                                   dot_1[6][0]                      
                                                                   lstm_1[5][0]                     
                                                                   lstm_1[5][2]                     
                                                                   dot_1[7][0]                      
                                                                   lstm_1[6][0]                     
                                                                   lstm_1[6][2]                     
                                                                   dot_1[8][0]                      
                                                                   lstm_1[7][0]                     
                                                                   lstm_1[7][2]                     
                                                                   dot_1[9][0]                      
                                                                   lstm_1[8][0]                     
                                                                   lstm_1[8][2]                     
____________________________________________________________________________________________________
dense_2 (Dense)                  (None, 11)            1419        lstm_1[0][0]                     
                                                                   lstm_1[1][0]                     
                                                                   lstm_1[2][0]                     
                                                                   lstm_1[3][0]                     
                                                                   lstm_1[4][0]                     
                                                                   lstm_1[5][0]                     
                                                                   lstm_1[6][0]                     
                                                                   lstm_1[7][0]                     
                                                                   lstm_1[8][0]                     
                                                                   lstm_1[9][0]                     
====================================================================================================
Total params: 185,484
Trainable params: 185,484
Non-trainable params: 0
____________________________________________________________________________________________________

从上面的总结可以看出，从\(t = 0, \ldots, T_y-1\)每一步，在dot_2计算内容向量之前，attention_weights 输出维度为(m, 30, 1)的 alphas。

函数attention_map()实现了从模型中提取出注意力值，并绘制出来。

1
attention_map = plot_attention_map(model, human_vocab, inv_machine_vocab, "Tuesday April 08 1993", num = 6, n_s = 128)
<matplotlib.figure.Figure at 0x7fc614061fd0>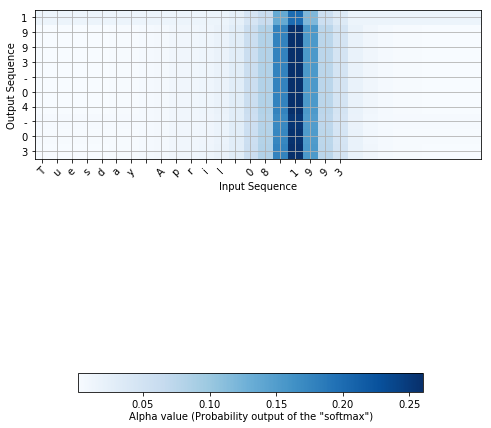
png

png

从上面的图中可以分析网络的输出对输入的哪一部分施加的注意力。

小结

  • 机器翻译模型可以用来将一个序列映射到另一个序列，它不仅在翻译人类语言（比如法语到英语）中十分有用，而且在日期格式翻译这样的任务中也有应用
  • 注意力机制允许一个网络在生成输出的特定部分时，只关注输入的相关部分
  • 基于注意力机制的网络可以将长度为\(T_x\)的输入，映射为长度为\(T_y\)的输出，其中\(T_x\)和\(T_y\)可以不同
  • 可视化注意力权重\(\alpha^{\langle t,t' \rangle}\)，可以获得在生成每个输出时网络所关注的输入部分

参考资料