排序算法及Python实现

发表于 | 分类于

本文将介绍几种经典的排序算法及Python实现，并对比它们的时间复杂度、空间复杂度和稳定性。

排序算法稳定性的简单形式化定义为：如果Ai = Aj，排序前Ai在Aj之前，排序后Ai还在Aj之前，则称这种排序算法是稳定的。通俗地讲就是保证排序前后两个相等的数的相对顺序不变。

对于不稳定的排序算法，只要举出一个实例，即可说明它的不稳定性；而对于稳定的排序算法，必须对算法进行分析从而得到稳定的特性。需要注意的是，排序算法是否为稳定的是由具体算法决定的，不稳定的算法在某种条件下可以变为稳定的算法，而稳定的算法在某种条件下也可以变为不稳定的算法。

例如，对于冒泡排序，原本是稳定的排序算法，如果将记录交换的条件改成A[i] >= A[i + 1]，则两个相等的记录就会交换位置，从而变成不稳定的排序算法。

其次，说一下排序算法稳定性的好处。排序算法如果是稳定的，那么从一个键上排序，然后再从另一个键上排序，前一个键排序的结果可以为后一个键排序所用。基数排序就是这样，先按低位排序，逐次按高位排序，低位排序后元素的顺序在高位也相同时是不会改变的。

冒泡法排序

原理

  1. 比较相邻的元素，如果前一个比后一个大，就把它们两个调换位置。
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

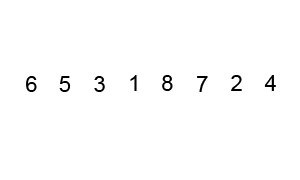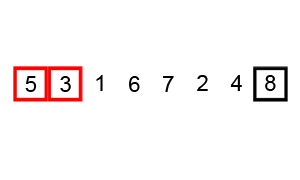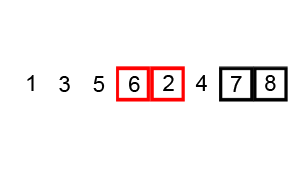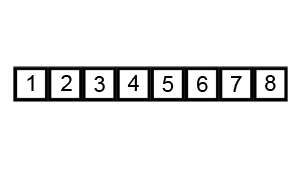
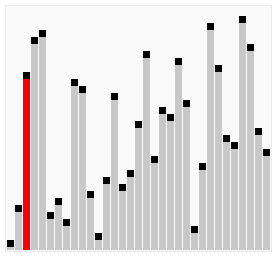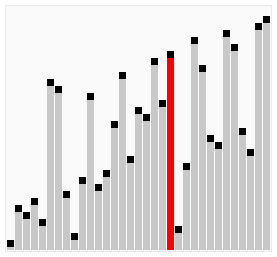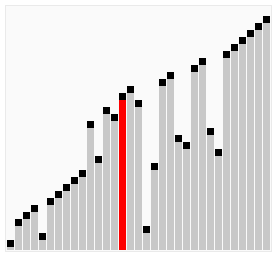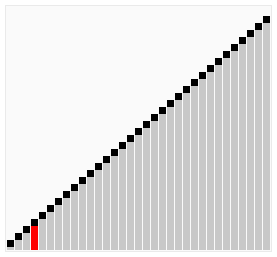### 特点 - 时间复杂度：\(O(n^2)\)

  • 空间复杂度：\(O(1)\)

  • 稳定性：稳定

1
2
3
4
5
6
def bubbleSort(arr):
    for i in range(len(arr)):
        for j in range(len(arr)-i-1):
            if arr[j] > arr[j+1]: 
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr
1
2
a = [10, 9, 7, 8, 20, 3, 4, 5]
print(bubbleSort(a))
[3, 4, 5, 7, 8, 9, 10, 20]

选择排序

原理

选择排序也是一种简单直观的排序算法。它的工作原理很容易理解：初始时在序列中找到最小（大）元素，放到序列的起始位置作为已排序序列；然后，再从剩余未排序元素中继续寻找最小（大）元素，放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

注意选择排序与冒泡排序的区别：冒泡排序通过依次交换相邻两个顺序不合法的元素位置，从而将当前最小（大）元素放到合适的位置；而选择排序每遍历一次都记住了当前最小（大）元素的位置，最后仅需一次交换操作即可将其放到合适的位置。 每次选择最小的值放在序列前面。包含两层循环，内循环选择最小的值，外循环为序列长度循环。

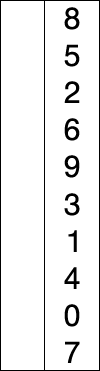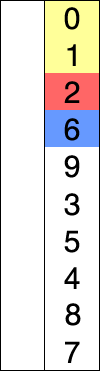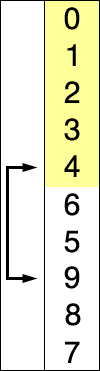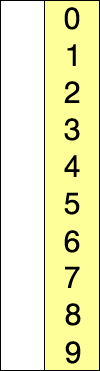
特点

  • 时间复杂度：\(O(n^2)\)

  • 空间复杂度：\(O(1)\)

  • 稳定性：不稳定
    比如序列：{ 5, 8, 5, 2, 9 }，一次选择的最小元素是2，然后把2和第一个5进行交换，从而改变了两个元素5的相对次序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def findSmallest(arr):
    """
    寻找数组中最小的元素
    """
    smallest = arr[0]
    smallest_indx = 0
    for i in range(1, len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_indx = i
    return smallest_indx

def selectionSort(arr):
    newArr = []
    for i in range(len(arr)):
        smallest = findSmallest(arr)
        newArr.append(arr.pop(smallest)) # 弹出最小值，并放在排序后的数组上
    return newArr
1
2
a = [10, 9, 7, 8, 20, 3, 4, 5]
print(selectionSort(a))
[3, 4, 5, 7, 8, 9, 10, 20]

插入排序

原理

插入排序是一种简单直观的排序算法。它的工作原理非常类似于我们抓扑克牌 对于未排序数据(右手抓到的牌)，在已排序序列(左手已经排好序的手牌)中从后向前扫描，找到相应位置并插入。

插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

具体算法描述如下：

  1. 从第一个元素开始，该元素可以认为已经被排序
  2. 取出下一个元素，在已经排序的元素序列中从前向后扫描
  3. 如果该元素（已排序）大于新元素，将该元素移到下一位置
  4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置
  5. 将新元素插入到该位置后
  6. 重复步骤2~5

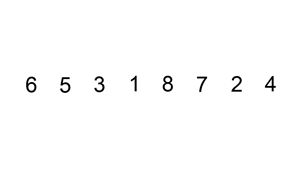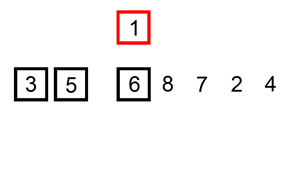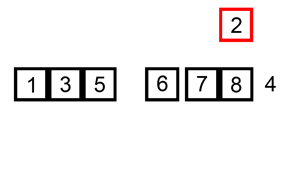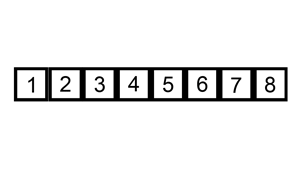
特点

  • 时间复杂度：\(O(n^2)\)

  • 空间复杂度：\(O(1)\)

  • 稳定性：稳定

1
2
3
4
5
6
7
def insertSort(array):
    for i in range(len(array)):
        for j in range(i):
            if array[i] < array[j]:
                array.insert(j, array.pop(i))
                break
    return array
1
2
a = [10, 9, 7, 8, 20, 3, 4, 5]
print(insertSort(a))
[3, 4, 5, 7, 8, 9, 10, 20]

快速排序

原理

快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序n个元素要O(nlogn)次比较。在最坏状况下则需要O(n^2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他O(nlogn)算法更快，因为它的内部循环可以在大部分的架构上很有效率地被实现出来。

快速排序使用分治策略(Divide and Conquer)来把一个序列分为两个子序列。步骤为：

  1. 从序列中挑出一个元素，作为"基准"(pivot)
  2. 把所有比基准值小的元素放在基准前面，所有比基准值大的元素放在基准的后面（相同的数可以到任一边），这个称为分区(partition)操作
  3. 对每个分区递归地进行步骤1~2，递归的结束条件是序列的大小是0或1，这时整体已经被排好序了

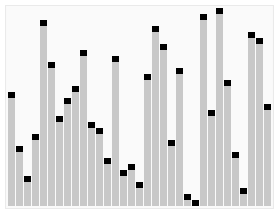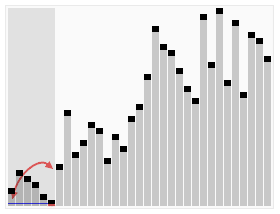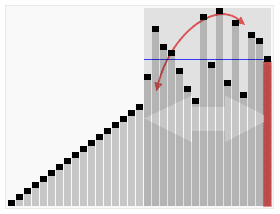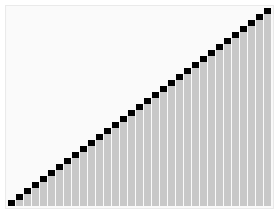
特点

  • 时间复杂度：\(O(nlogn)\)

  • 空间复杂度：\(O(nlogn)\)

  • 不稳定
    快速排序是不稳定的排序算法， 比如序列：{ 1, 3, 4, 2, 8, 9, 8, 7, 5 }，基准元素是5，一次划分操作后5要和第一个8进行交换，从而改变了两个元素8的相对次序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def quickSort(array):
    """
    递归算法实现快速排序
    """
    # 基线条件
    if len(array) < 2:
        return array
    # 递归条件
    else:
        pivot = array[0]
        # 所有小于基准值的元素组成的子数组
        less = [i for i in array[1:] if i <= pivot]
        # 所有大于基准值的元素组成的子数组
        greater = [i for i in array[1:] if i > pivot]
        return quickSort(less) + [pivot] + quickSort(greater)
1
2
a = [10, 9, 7, 8, 20, 3, 4, 5]
print(quickSort(a))
[3, 4, 5, 7, 8, 9, 10, 20]

总结

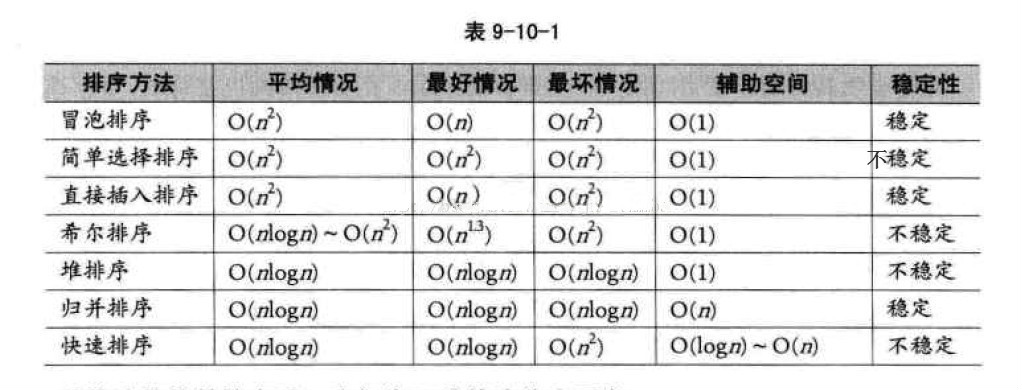
参考资料

1.常用排序算法总结

2.Python八大排序算法速度比较